Задание 1. Вычислить площадь фигуры, ограниченной линиями, заданными в декартовой системе координат:
| 1.1. | гиперболой 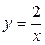 и прямой и прямой 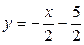 ; ; | 1.2. | 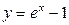 , , 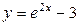 , , 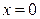 ; ; |
| 1.3. | 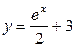 , , 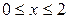 ; ; | 1.4. | 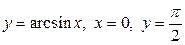 ; ; |
| 1.5. | 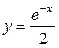 , , 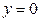 , , 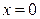 , , 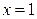 ; ; | 1.6. | параболой 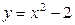 и прямыми и прямыми 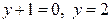 ; ; |
| 1.7. | 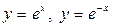 , , 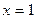 ; ; | 1.8. | 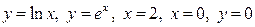 ; ; |
| 1.9. | параболами 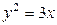 и и 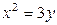 ; ; | 1.10. | параболой 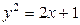 и прямой и прямой 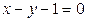 ; ; |
| 1.11. | параболой 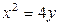 и локоном Аньези и локоном Аньези 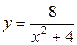 ; ; | 1.12. | параболой 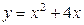 и прямой и прямой 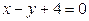 ; ; |
| 1.13. | параболами 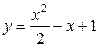 и и 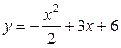 ; ; | 1.14. | кубической параболой 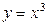 и прямыми и прямыми 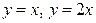 ; ; |
| 1.15. | параболой 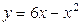 и прямой и прямой 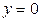 ; ; | 1.16. | 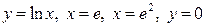 ; ; |
| 1.17. | кубической параболой 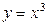 и прямыми и прямыми 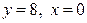 ; ; | 1.18. | параболами 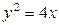 и и 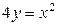 ; ; |
| 1.19. | параболой 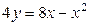 и прямой и прямой 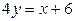 ; ; | 1.20. | параболой 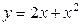 и прямой и прямой 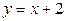 ; ; |
| 1.21. | параболой 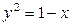 и прямой и прямой 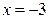 ; ; | 1.22. | параболой 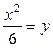 и локоном Аньези и локоном Аньези 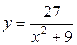 ; ; |
| 1.23. | гиперболой 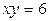 и прямой и прямой 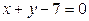 ; ; | 1.24. | параболами 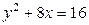 и и 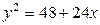 ; ; |
| 1.25. | параболами 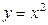 и и 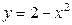 ;. ;. | 1.26. | параболами 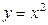 и и 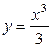 ; ; |
| 1.27. | параболами 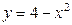 и и 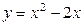 ; ; | 1.28. | параболой 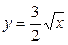 , гиперболой , гиперболой 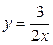 и прямыми и прямыми 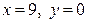 ; ; |
| 1.29. | полукубической параболой 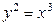 и прямыми и прямыми 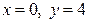 ; ; | 1.30. | 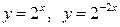 и и 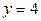 . . |
Задание 2. Вычислить площадь фигуры, ограниченной линиями, заданными параметрически
| 2.1. | астроидой 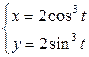 ; ; | 2.2. | астроидой 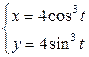 ; ; |
| 2.3. | эллипсом 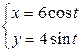 ; ; | 2.4. | эллипсом 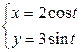 с условием с условием 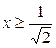 ; ; |
| 2.5. | первой аркой циклоиды 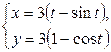 и прямой y=0; и прямой y=0; | 2.6. | петли 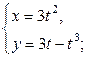 |
| 2.7. | 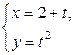 и прямыми и прямыми 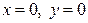 ; ; | 2.8. | астроидой 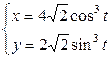 с условием с условием 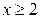 ; ; |
| 2.9. | эллипсом 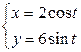 с условием с условием 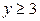 ; ; | 2.10. | эллипсом 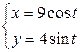 с условием с условием 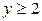 ; ; |
| 2.11 | первой аркой циклоиды 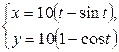 с условием с условием 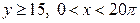 ; ; | 2.12. | первой аркой циклоиды 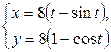 с условием с условием 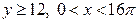 ; ; |
| 2.13. | эллипсом 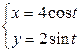 с условием с условием 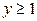 ; ; | 2.14. | первой аркой циклоиды 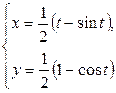 , при условии , при условии 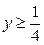 ; ; |
| 2.15. | эллипсом 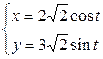 с условием с условием 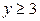 ; ; | 2.16. | астроидой 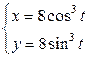 с условием с условием 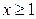 ; ; |
| 2.17. | астроидой 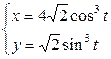 с условием с условием 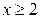 ; ; | 2.18. | первой аркой циклоиды 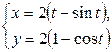 с условием с условием 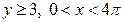 ; ; |
| 2.19. | первой аркой циклоиды 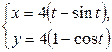 с условием с условием 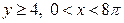 ; ; | 2.20. | петли 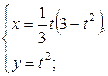 |
| 2.21. | эллипсом 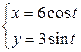 с условием с условием 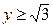 ; ; | 2.22. | астроидой 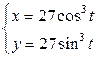 ; ; |
| 2.23. | первой аркой циклоиды 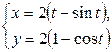 и осью Ох; и осью Ох; | 2.24. | астроидой 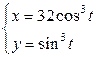 с условием с условием 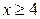 ; ; |
| 2.25. | петли 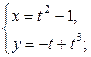 | 2.26. | эллипсом 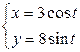 с условием с условием 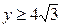 ; ; |
| 2.27. | астроидой 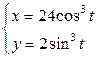 с условием с условием 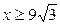 ; ; | 2.28. | первой аркой циклоиды 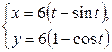 с условием с условием 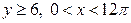 ; ; |
| 2.29. | эллипсом 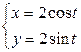 с условием с условием 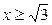 ; ; | 2.30. | петли 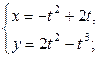 |
Задание 3. Вычислить площадь фигуры, ограниченной линиями, заданными в полярной системе координат:
| 3.1. | Лемнискатой Бернулли 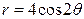 ; ; | 3.2. | трехлепестковой розой 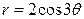 ; ; |
| 3.3. | трехлепестковой розой 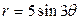 ; ; | 3.4. | четырехлепестковой розой 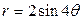 ; ; |
| 3.5. | окружностями 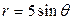 , , 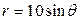 ; ; | 3.6. | окружностями 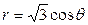 , , 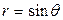 ; ; |
| 3.7. | кардиоидой 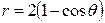 и окружностью r=2; и окружностью r=2; | 3.8. | окружностью 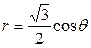 , с условием , с условием 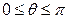 ; ; |
| 3.9. | Лемнискатой Бернулли 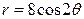 ; ; | 3.10. | трехлепестковой розой 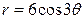 ; ; |
| 3.11 | трехлепестковой розой 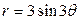 ; ; | 3.12. | четырехлепестковой розой 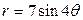 ; ; |
| 3.13. | окружностями 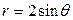 , , 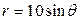 ; ; | 3.14. | окружностями 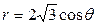 , , 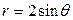 ; ; |
| 3.15. | кардиоидой 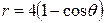 и окружностью r=4; и окружностью r=4; | 3.16. | окружностью 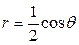 , с условием , с условием 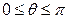 ; ; |
| 3.17. | кардиоидой 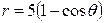 ; ; | 3.18. | трехлепестковой розой 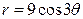 ; ; |
| 3.19. | Лемнискатой Бернулли 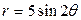 ; ; | 3.20. | четырехлепестковой розой 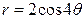 ; ; |
| 3.21. | трехлепестковой розой 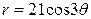 ; ; | 3.22. | окружностями 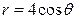 , , 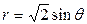 ; ; |
| 3.23. | окружностями 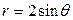 , , 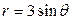 ; ; | 3.24. | окружностью 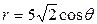 , с условием , с условием 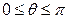 ; ; |
| 3.25. | кардиоидой 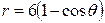 и окружностью r=6; и окружностью r=6; | 3.26. | окружностями 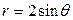 , , 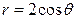 ; ; |
| 3.27. | Лемнискатой Бернулли 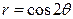 ; ; | 3.28. | кардиоидой 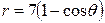 ; ; |
| 3.29. | трехлепестковой розой 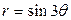 ; ; | 3.30. | четырехлепестковой розой 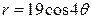 . . |
Задание 4. Вычислить несобственный интеграл, если он сходится, или установить его расходимость:
| 4.1. | 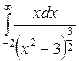 ; ; | 4.2. | 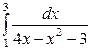 ; ; |
| 4.3. | 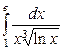 ; ; | 4.4. | 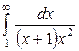 ; ; |
| 4.5. | 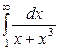 ; ; | 4.6. | 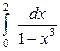 ; ; |
| 4.7. | 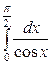 ; ; | 4.8. | 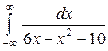 : : |
| 4.9. | 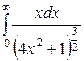 ; ; | 4.10. | 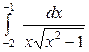 ; ; |
| 4.11 | 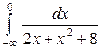 ; ; | 4.12. | 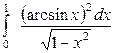 ; ; |
| 4.13. | 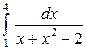 ; ; | 4.14. | 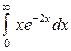 ; ; |
| 4.15. | 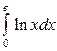 ; ; | 4.16. | 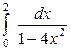 ; ; |
| 4.17. | 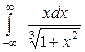 ; ; | 4.18. | 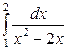 ; ; |
| 4.19. | 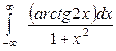 ; ; | 4.20. | 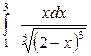 ; ; |
| 4.21. | 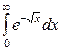 ; ; | 4.22. | 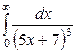 ; ; |
| 4.23. | 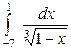 ; ; | 4.24. | 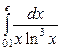 ; ; |
| 4.25. | 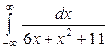 ; ; | 4.26. | 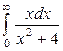 ; ; |
| 4.27. | 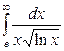 ; ; | 4.28. | 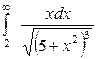 ; ; |
| 4.29. | 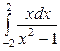 ; ; | 4.30. | 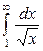 ; ; |
Задание 5. Вычислить длину дуги кривой, заданной в декартовых координатах:
| 5.1. | 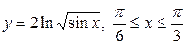 ; ; | 5.2. | 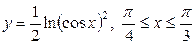 ; ; |
| 5.3. | 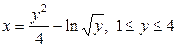 ; ; | 5.4. | 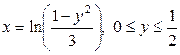 ; ; |
| 5.5. | 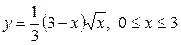 ; ; | 5.6. | 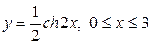 ; ; |
| 5.7. | 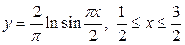 ; ; | 5.8. | 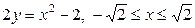 ; ; |
| 5.9. | 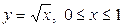 ; ; | 5.10. | 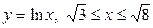 ; ; |
| 5.11 | 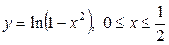 ; ; | 5.12. | 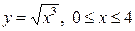 ; ; |
| 5.13. | 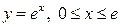 ; ; | 5.14. | 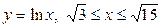 ; ; |
| 5.15. | 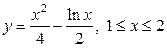 ; ; | 5.16. | 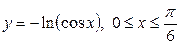 ; ; |
| 5.17. | 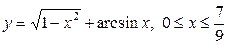 ; ; | 5.18. | 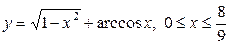 ; ; |
| 5.19. | 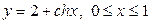 ; ; | 5.20. | 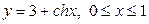 ; ; |
| 5.21. | 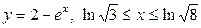 ; ; | 5.22. | 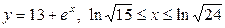 ; ; |
| 5.23. | 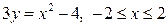 ; ; | 5.24. | 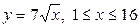 ; ; |
| 5.25. | 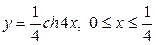 ; ; | 5.26. | 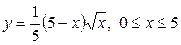 ; ; |
| 5.27. | 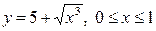 ; ; | 5.28. | 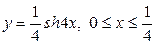 |
| 5.29. | 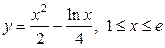 ; ; | 5.30. | 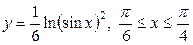 |
Задание 6. Вычислить длину дуги кривой, заданной параметрически:
| 6.1. | 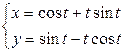 , от , от 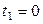 до до 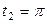 ; ; | 6.2. | 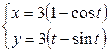 , от , от 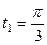 до до 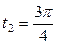 ; ; |
| 6.3. | 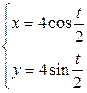 , , 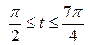 ; ; | 6.4. | 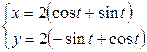 , от , от 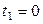 до до 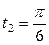 ; ; |
| 6.5. | 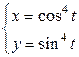 , , 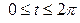 ; ; | 6.6. | 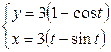 , от , от 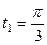 до до 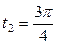 ; ; |
| 6.7. | 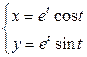 , , 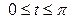 ; ; | 6.8. | части петли 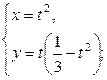 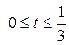 ; ; |
| 6.9. | 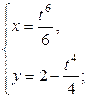 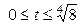 ; ; | 6.10. | 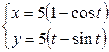 , от , от 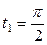 до до 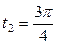 ; ; |
| 6.11. | 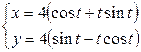 , от , от 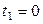 до до 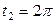 ; ; | 6.12. | 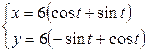 , от , от 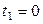 до до 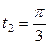 ; ; |
| 6.13. | 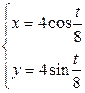 , , 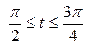 ; ; | 6.14. | 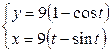 , от , от 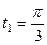 до до 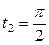 ; ; |
| 6.15. | 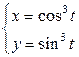 , , 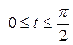 ; ; | 6.16. | части петли 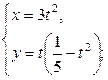 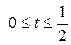 ; ; |
| 6.17. | 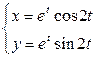 , , 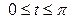 ; ; | 6.18. | 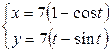 , от , от 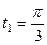 до до 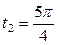 ; ; |
| 6.19. | 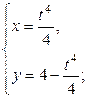 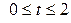 ; ; | 6.20. | 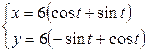 , от , от 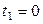 до до 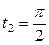 ; ; |
| 6.21. | 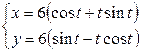 , от , от 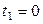 до до 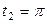 ; ; | 6.22. | 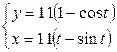 , от , от 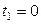 до до 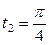 ; ; |
| 6.23. | 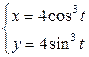 , , 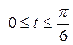 ; ; | 6.24. | 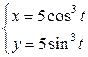 , , 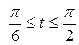 ; ; |
| 6.25. | 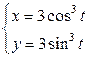 , , 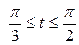 ; ; | 6.26. | 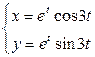 , , 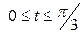 ; ; |
| 6.27. | 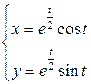 , , 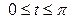 ; ; | 6.28. | 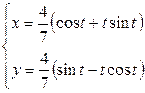 , от , от 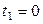 до до 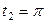 ; ; |
| 6.29. | 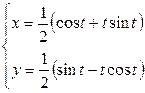 , от , от 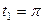 до до 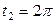 ; ; | 6.30. | 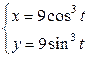 , , 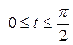 ; ; |
Задание 7. Вычислить длину дуги кривой, заданной в полярных координатах:
| 7.1. | 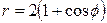 , , 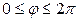 ; ; | 7.2. | 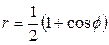 , , 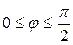 ; ; |
| 7.3. | 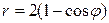 , , 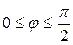 ; ; | 7.4. | 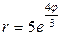 , , 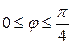 ; ; |
| 7.5. | 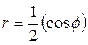 , , 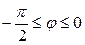 ; ; | 7.6. | 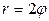 , , 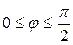 ; ; |
| 7.7. | 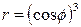 , , 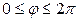 ; ; | 7.8. | 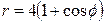 , , 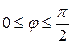 ; ; |
| 7.9. | 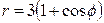 , , 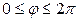 ; ; | 7.10. | 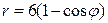 , , 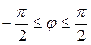 ; ; |
| 7.11 | 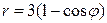 , , 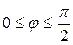 ; ; | 7.12. | 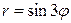 , , 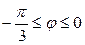 ; ; |
| 7.13. | 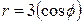 , , 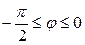 ; ; | 7.14. | 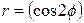 , , 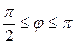 ; ; |
| 7.15. | 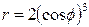 , , 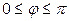 ; ; | 7.16. | 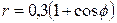 , , 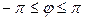 ; ; |
| 7.17. | 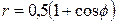 , , 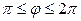 ; ; | 7.18. | 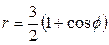 , , 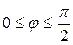 ; ; |
| 7.19. | 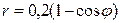 , , 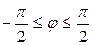 ; ; | 7.20. | 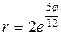 , , 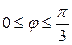 ; ; |
| 7.21. | 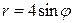 , , 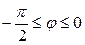 ; ; | 7.22. | 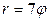 , , 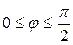 ; ; |
| 7.23. | 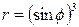 , , 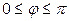 ; ; | 7.24. | 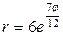 , , 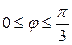 ; ; |
| 7.25. | 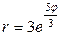 , , 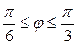 ; ; | 7.26. | 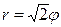 , , 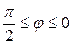 ; ; |
| 7.27. | 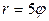 , , 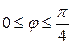 ; ; | 7.28. | 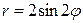 , , 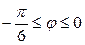 ; ; |
| 7.29. | 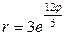 , , 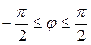 ; ; | 7.30. | 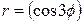 , , 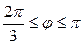 . . |
Задание 8. Вычислить объем тела вращения вокруг указанной оси:
| 8.1. | 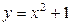 , , 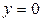 , , 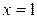 , , 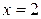 ; ОХ ; ОХ | 8.2. | 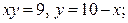 ОY ОY |
| 8.3. | 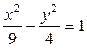 , , 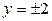 ; ОY ; ОY | 8.4. | 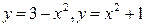 ; ОY ; ОY |
| 8.5. | 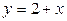 , , 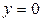 , , 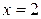 ; ОХ ; ОХ | 8.6. | 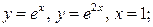 ОХ ОХ |
| 8.7. | 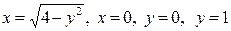 ; ОY ; ОY | 8.8. | 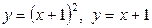 ; ОХ ; ОХ |
| 8.9. | 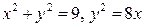 ; ОХ ; ОХ | 8.10. | 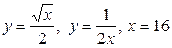 ; ОХ ; ОХ |
| 8.11 | 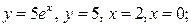 ОХ ОХ | 8.12. | 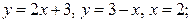 ОХ ОХ |
| 8.13. | 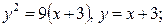 ОХ ОХ | 8.14. | 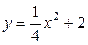 , , 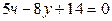 ; ОХ ; ОХ |
| 8.15. | 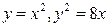 ; ОY ; ОY | 8.16. | 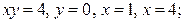 ОХ ОХ |
| 8.17. | 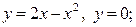 ОХ ОХ | 8.18. | 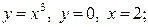 ОY ОY |
| 8.19. | 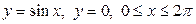 ; ОХ ; ОХ | 8.20. | 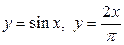 ; ОХ ; ОХ |
| 8.21. | 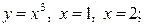 ОХ ОХ | 8.22. | 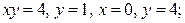 ОY ОY |
| 8.23. | 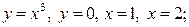 ОY ОY | 8.24. | 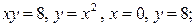 ОY ОY |
| 8.25. | 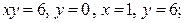 ОХ ОХ | 8.26. | 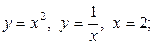 ОY ОY |
| 8.27. | 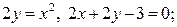 ОХ ОХ | 8.28. | 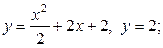 ОY ОY |
| 8.29. | 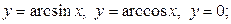 ОY ОY | 8.30. | 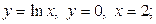 ОY ОY |
Задание 9. Вычислить определенный интеграл, используя способ замены переменной:
| 9.1. | 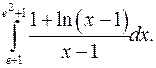 | 9.2. | 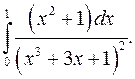 |
| 9.3. | 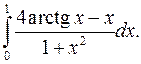 | 9.4. | 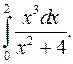 |
| 9.5. | 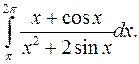 | 9.6. | 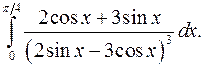 |
| 9.7. | 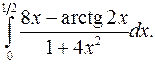 | 9.8. | 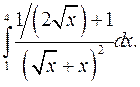 |
| 9.9. | 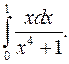 | 0.10. | 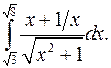 |
| 9.11. | 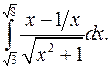 | 9.12. | 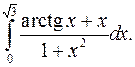 |
| 9.13. | 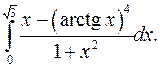 | 9.14. | 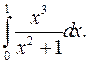 |
| 9.15. | 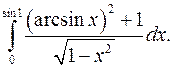 | 9.16. | 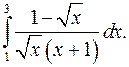 |
| 9.17. | 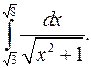 | 9.18. | 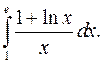 |
| 9.19. | 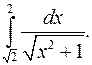 | 9.20. | 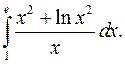 |
| 9.21. | 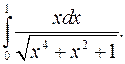 | 9.22. | 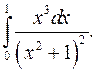 |
| 9.23. | 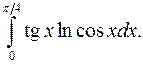 | 9.24. | 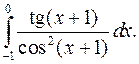 |
| 9.25. | 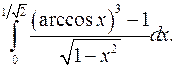 | 9.26. | 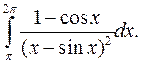 |
| 9.27. | 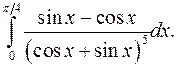 | 9.28. | 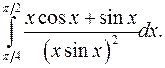 |
| 9.29. | 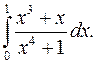 | 9.30. | 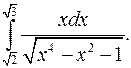 |
Задание 10. Вычислить определенный интеграл, используя метод интегрирования по частям.
| 10.1. | 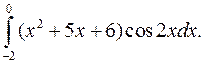 | 10.2. | 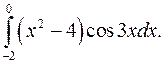 |
| 10.3. | 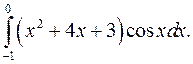 | 10.4. | 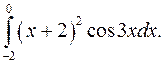 |
| 10.5 | 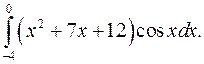 | 10.6. | 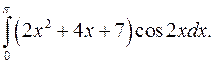 |
| 10.7. | 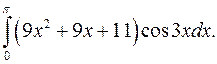 | 10.8. | 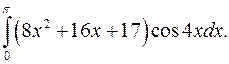 |
| 10.9. | 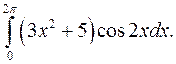 | 10.10. | 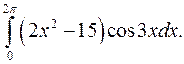 |
| 10.11. | 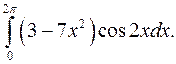 | 10.12. | 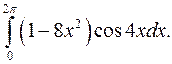 |
| 10.13. | 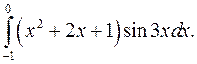 | 10.14. | 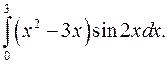 |
| 10.15. | 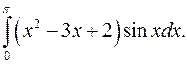 | 10.16. | 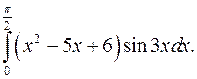 |
| 10.17. | 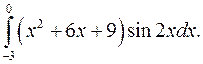 | 10.18. | 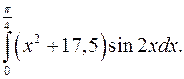 |
| 10.19. | 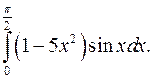 | 10.20. | 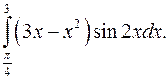 |
| 10.21. | 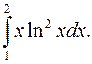 | 10.22. | 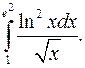 |
| 10.23. | 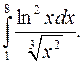 | 10.24. | 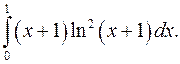 |
| 10.25. | 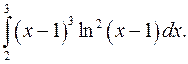 | 10.26. | 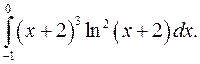 |
| 10.27. | 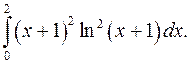 | 10.28. | 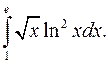 |
| 10.29. | 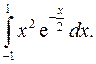 | 10.30. | 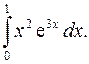 |
 2015-05-30
2015-05-30 1637
1637








