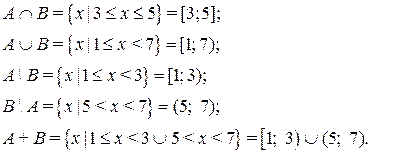Решение задач по теории множеств, доказательство формул удобно проводить, пользуясь не только определениями и объектным представлением о множестве, но и с помощью диаграмм Эйлера. Рассмотрим решения ряда типовых задач.
1. Определить множество А решений уравнения х2 – 25 = 0.
x 2 – 25 = 0 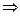 х 2 = 25
х 2 = 25 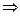 х 1 = –5; х 2 = 5.
х 1 = –5; х 2 = 5.
Ответ: А ={ x | x 2 – 25 = 0}={–5; 5}.
2. Определить множество В решений неравенства 2х + 9 ³ 0.
2 х + 9 ³ 0 Þ 2 x ³ – 9 Þ 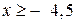 .
. 

Ответ: В ={ x | 2 х +9 ³ 0}={ х | x ³ – 4,5}= 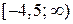 .
.
3. Заданы множества 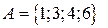 и
и 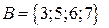 . Определить результаты операций
. Определить результаты операций  .
.
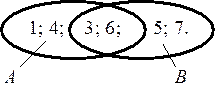 |
Изобразим эти множества диаграммами Эйлера и решим задачу:
Решение:

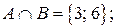
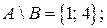
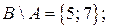
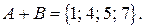
4. Определить результаты тех же операций, если 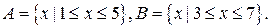
|
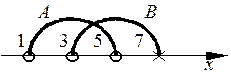
5. Доказать формулу 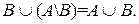
Рассмотрим на диаграмме, что будет результатом для левой части формулы:
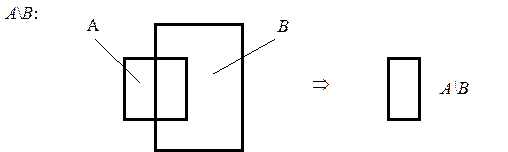
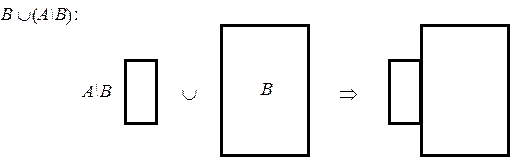
Результат для правой части:

Так как оба рисунка полностью совпали, то формула - доказана.
6. Определить все подмножества множества А = {0; 1; 3}.
Несобственные: Æ и А; одноэлементные: {0}, {1}, {3}; двухэлементные: {0; 1}, {0; 3}, {1; 3}.
Следовательно, множество-степень Р (А), т.е. множество всех подмножеств, имеет вид Р (А) = {Æ; {0}; {1}; {3}; {0; 1}; {0; 3}; {1; 3}; {0; 1; 3}}.
Для проверки используем теорему: если множество А состоит из n элементов, то число всех его подмножеств равно 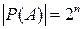 .
.
Для нашего примера n = 3, следовательно число подмножеств 23 = 8, что совпадает с числом объектов в Р (А).
7. Оценить множество А = {2; 6; 1; 8}.
В этом множестве легко найти: max A = 8; min A = 1; sup A = 8; inf A = 1.
8. Оценить множество N = {1; 2; 3;…}, т.е. натуральный ряд.
Здесь min N = 1; max N – не существует; sup N – не существует (sup N = ¥); inf N = 1.
9. Оценить множество А={х| 2 £x < 5}.
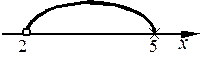 |
Из рисунка следует: min А = 2; max A – не существует, т.к. 5 Ï А; sup A = 5; inf A = 2.
10. Оценить множество А={х | 3 < x < ¥ }.
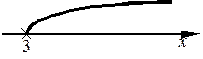 |
Здесь min A – не существует, т.к. 3 Ï А; max A – не существует; inf A = 3; sup A – не существует (sup A = ¥).
Рассмотрим теперь примеры вычислений с комплексными числами. Множество С, имеющее широкое распространение во многих разделах математического анализа, во многом аналогично множеству действительных чисел, но требует аккуратной записи результатов вычислений.
11. Упростить (1 - 2i)(2 + i)2 + 5i.
Последовательно:
(2 + i) 2= 4 + 4 i + i2 = 4 + 4 i – 1 = 3 + 4 i;
(1 - 2 i)(2 + i) 2 = (1 - 2 i)(3 + 4 i) = 3 - 6 i + 4 i - 8i2 = 3 - 2 i + 8 = 11 - 2 i.
В итоге 11 - 2 i + 5 i = 11 + 3 i.
Ответ: 11 + 3 i.
12. Упростить 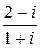 .
.
Напомним, что результат операций с комплексными числами всегда должен представляться в виде a+bi. Для ликвидации знаменателя умножим числитель и знаменатель этой дроби на сопряженное знаменателю комплексное число 1-i:
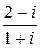
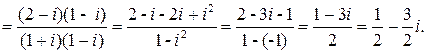
Ответ: 0,5 - 1,5 i.
В случае более громоздкого выражения, например, 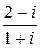
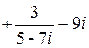 , сначала необходимо привести все выражение к общему знаменателю; раскрывая скобки, упростить до дроби, а затем умножить на сопряженное знаменателю число.
, сначала необходимо привести все выражение к общему знаменателю; раскрывая скобки, упростить до дроби, а затем умножить на сопряженное знаменателю число.
13. Найти действительные решения уравнения:
(1 + i)x + (-2 + 5i)y = -4 + 17i.
Преобразуем левую часть:
(1 + i) x + (-2 + 5 i) y = x + xi - 2 y + 5 yi = (x - 2 i) + (x + 5 y) i,
т.е. (x - 2 i) + (x + 5 y) i = -4 + 17 i.
По теореме о равенстве комплексных чисел получаем систему уравнений:
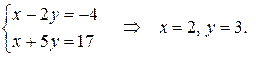
Ответ: х = 2; у = 3.
14. Изобразить на комплексной плоскости и представить в тригонометрической форме комплексные числа 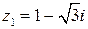 и
и 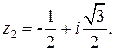
Выберем способ изображения комплексных чисел как радиус-векторов. Тогда: z1 = (1; - 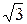 ) и z2 = (-0,5; 0,5
) и z2 = (-0,5; 0,5 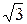 ).
).
Для z1: модуль и аргумент 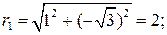 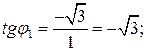 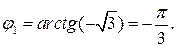 По чертежу - приводя к четвертой четверти, получим По чертежу - приводя к четвертой четверти, получим 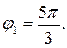 Следовательно, Следовательно, 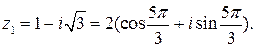 |
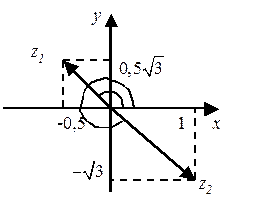
Для z2: модуль и аргумент
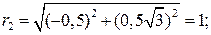
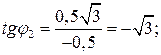 =
= 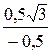 = -
= - 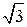 ;
; 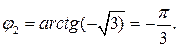
По чертежу - приводя к второй четверти, получим 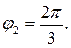
Следовательно, 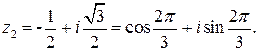
15. Пусть z1 = 3 + 2i; z2 = 2 + 2i. Вычислить z1 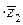 .
.
Найдем сопряженное к z2 число: 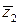 = 2 - 2 i
= 2 - 2 i 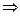 z1
z1 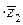 = (3 + 2 i)(2 - 2 i) =
= (3 + 2 i)(2 - 2 i) =
= 6 + 4 i - 6 i - 4 i2 = 6 - 2 i + 4 = 10 - 2 i.
Ответ: 10 - 2 i.
16. Вычислить  .
.
Так как результатом этой операции опять будет комплексное число, запишем:
 = x + yi
= x + yi 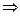 -2 + i = (x + yi)2
-2 + i = (x + yi)2 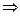 -2 + i = (x2 - y2) + 2 xyi.
-2 + i = (x2 - y2) + 2 xyi.
По теореме о равенстве комплексных чисел имеем систему:
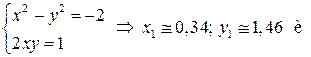
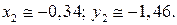
Ответ: 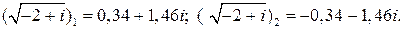
17. Решить уравнение z2 + 2z + 5 = 0.
Решение: 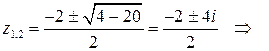 z1 = -1 + 2 i; z2 = -1 - 2 i.
z1 = -1 + 2 i; z2 = -1 - 2 i.
Ответ: z1 = -1 + 2 i; z2 = 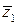 = -1 - 2 i.
= -1 - 2 i.
Контрольные вопросы
1. Понятие множества.
2. Обозначения. Изображения множеств.
3. Способы задания множеств.
4. Подмножества. Собственные и несобственные подмножества.
5. Операции над множествами и свойства операций.
6. Декартово произведение множеств и его свойства.
7. Соответствие, отображение и функция.
8. Обратное отображение.
9. Мощность множества.
10. Счетное и несчетное множества.
11. Множество-степень, формула числа подмножеств.
12. Основные числовые множества.
13. Ограниченные и неограниченные множества.
14. Максимум и минимум множества.
15. Грани множества.
16. Мнимая единица и ее свойства.
17. Определение комплексного числа.
18. Свойства и изображение комплексных чисел.
19. Модуль и аргумент комплексного числа.
20. Тригонометрическая форма комплексного числа.
22. Сложение, умножение, деление и возведение в степень комплексных чисел.
23. Извлечение корня из комплексного числа.
24. Сопряженные комплексные числа и их свойства.
25. Решение алгебраических уравнений.
 2015-05-22
2015-05-22 5477
5477