{ а, b, с,... } – множество, состоящее из элементов а, b, c, …
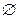 – пустое множество;
– пустое множество;
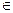 – знак принадлежности множеству;
– знак принадлежности множеству;
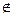 – знак непринадлежности множеству;
– знак непринадлежности множеству;
{ х | х 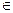 N },–множество элементов x, удовлетворяющих условию х
N },–множество элементов x, удовлетворяющих условию х 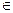 N;
N;
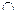 – знак пересечения множеств;
– знак пересечения множеств;
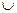 – знак объединения множеств;
– знак объединения множеств;
\ – знак разности множеств (А \ В);
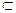 – знак включения;
– знак включения;
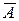 – дополнение множества А в множестве Х;
– дополнение множества А в множестве Х;
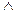 – союз «и»;
– союз «и»;
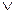 – союз «или»;
– союз «или»;
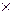 – знак прямого (декартового) произведения;
– знак прямого (декартового) произведения;
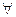 – квантор общности;
– квантор общности;
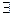 – квантор существования;
– квантор существования;
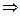 – знак логического следования;
– знак логического следования;
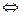 – знак равносильности (эквивалентности);
– знак равносильности (эквивалентности);
R – множество действительных чисел;
N – множество натуральных чисел;
Z — множество целых чисел;
Q – множество рациональных чисел.
Глава I. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
§1. Множества.
Подсознательно первые представления о множестве у человека начинают формироваться с рождения, когда он погружается в удивительно многообразный мир окружающих его объектов и явлений. В нем уже генетически заложены возможности ускоренно воспроизвести весь опыт общения с этим миром, накопленный человечеством за многовековую историю. Уникальность этого генетического потенциала, прежде всего, и отличает человека от других существ. С первых же шагов мы не просто пополняем список знакомых нам объектов и явлений, а начинаем дифференцировать и классифицировать (горячие и холодные, сладкие и горькие, тяжелые и легкие, красные и зеленые и т.п.), объединяя тем самым объекты в некоторые совокупности. Первый же опыт общения с ними убеждает нас и в том, что каждый объект имеет сложную структуру (кто из нас не ломал ни одной игрушки, пытаясь выяснить, из чего она состоит), представляет собой как бы определенную совокупность других объектов, из которых, как из составляющих, состоит сам. Поэтому понятие множества является ключевым в математике, без которого невозможно изложение ни одного из ее разделов. Множество — первичное понятие математики, т. е. это понятие не определяется через другие, а только поясняется. Так, можно говорить о множестве людей, живущих на нашей планете в данный момент времени, о множестве точек данной геометрической фигуры, о множестве решений данного уравнения. Люди, живущие на нашей планете в данный момент времени, точки данной геометрической фигуры, решение данного уравнения являются элементами соответствующего множества. Множество — это совокупность каких-либо объектов. Объекты любой природы, входящие в данное множество, называются элементами множества. Элементами множеств могут быть самые разнообразные предметы: буквы, числа, функции, точки, углы, люди и т.д. Например, число 5 является элементом множества натуральных чисел, квадрат – элементом множества геометрических фигур, январь – элементом множества месяцев в году. Отсюда с самого начала ясна чрезвычайная широта теории множеств и ее применение к очень многим областям знания.
Создатель теории множеств Г. Кантор (1845-1918) определил множество как «объединение в одно целое объектов, хорошо различимых нашей интуицией или нашей мыслью», а также «множество есть многое, мыслимое нами как единое». Разумеется, эти слова не могут рассматриваться как математически строгое определение множества, такого определения не существует, поскольку понятие множества является исходным, на основании которого строятся остальные понятия математики, т.е. множество является основным строительным материалом математики.
Отношение между множеством и его элементом выражают при помощи слова «принадлежит». Для сокращения записи различных высказываний о множествах и их элементах принята следующая символика: множества обычно обозначаются большими буквами латинского алфавита 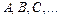 и т.д., а их элементы – малыми
и т.д., а их элементы – малыми 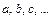 и т.д.; слово «принадлежит» заменяют символом «
и т.д.; слово «принадлежит» заменяют символом «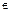 ». Высказывание «Объект
». Высказывание «Объект 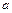 принадлежит множеству
принадлежит множеству  » записывают: «
» записывают: «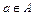 ». Эту запись можно прочитать иначе: «Объект
». Эту запись можно прочитать иначе: «Объект 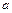 есть элемент множества
есть элемент множества  ». Высказывание «Объект
». Высказывание «Объект 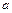 не принадлежит множеству
не принадлежит множеству  » записывают: «
» записывают: «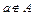 ». Эту запись можно прочитать иначе: «Объект
». Эту запись можно прочитать иначе: «Объект 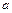 не является элементом множества
не является элементом множества  ». Для некоторых числовых множеств существуют специальные обозначения:
». Для некоторых числовых множеств существуют специальные обозначения: 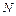 – множество натуральных чисел,
– множество натуральных чисел, 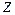 – множество целых чисел,
– множество целых чисел, 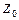 – множество целых неотрицательных чисел,
– множество целых неотрицательных чисел, 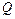 множество рациональных чисел,
множество рациональных чисел, 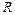 – множество всех действительных чисел.
– множество всех действительных чисел.
Множества, состоящие из конечного числа элементов (причем неважно, известно это число или нет, главное, что оно существует), называются конечными, а множества, состоящие из бесконечного числа элементов, — бесконечными. Например, множество дисциплин, изучаемых в институте, конечно, а множество точек прямой – бесконечно. Если множество не содержит ни одного элемента, то его называют пустым множеством и обозначают символом «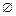 ». Пример пустого множества – множество людей, живущих на Солнце. Существует лишь одно пустое множество.
». Пример пустого множества – множество людей, живущих на Солнце. Существует лишь одно пустое множество.
Элементами множества также могут быть множества. Например, если говорить о множестве факультетов некоторого института, то элементы этого множества – группы, которые в свою очередь являются множествами студентов.
Определение: Множество  называется подмножеством множества
называется подмножеством множества  тогда и только тогда, когда каждый элемент множества
тогда и только тогда, когда каждый элемент множества  принадлежит множеству
принадлежит множеству  . Записывают: «
. Записывают: «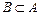 ». Можно сказать также:
». Можно сказать также:  включено в
включено в  , множество
, множество  содержится в
содержится в  . Согласно данному определению подмножества, каждое множество является подмножеством самого себя: «
. Согласно данному определению подмножества, каждое множество является подмножеством самого себя: «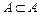 ». Пустое множество есть подмножество любого множества А: «
». Пустое множество есть подмножество любого множества А: «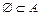 ».
».
Определение: Множества  и
и  называют равными, если они состоят из одних и тех же элементов. Обозначают: «
называют равными, если они состоят из одних и тех же элементов. Обозначают: «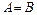 ». Например, множества
». Например, множества 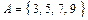 и
и 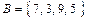 равны, так как состоят из одинаковых элементов.
равны, так как состоят из одинаковых элементов.
Очевидно, что если 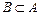 и
и 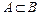 , то
, то 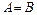 , т.е. если любой элемент из
, т.е. если любой элемент из  является элементом множества
является элементом множества  и любой элемент из
и любой элемент из  является элементом множества
является элементом множества  , то
, то 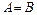 .
.
Если каждый элемент множества  является элементом множества
является элементом множества  , а каждый элемент множества
, а каждый элемент множества  является элементом множества
является элементом множества 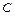 , то каждый элемент множества
, то каждый элемент множества  является элементом множества
является элементом множества 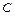 , т.е.
, т.е. 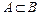 и
и 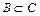 , то
, то 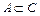 .
.
§ 2. Способы задания множеств. Операции над множествами
Множество считается заданным, если указано характеристическое свойство элементов этого множества, т.е. такое свойство, которым обладают все элементы этого множества и только они. Множество задают либо перечислением его элементов, либо описанием свойств множества, которые четко определяют совокупность его элементов. При втором способе множество обычно определяется как совокупность тех и только тех элементов из некоторого основного множества Т, которые обладают свойством а. В этом случае используют обозначение 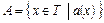 .
.
Множества, отношения между ними, операции над множествами и их свойства изображаются, обычно, с помощью диаграмм Эйлера – Венна, а бинарные отношения иллюстрируются на матрицах и графах. Благодаря этому основные понятия теории множеств можно представить в табличной или графической форме. Совокупность допустимых объектов называют универсальным множеством (обычно I). На диаграммах Эйлера – Веннауниверсальное множество I часто изображают в виде прямоугольника, а его подмножества – кругами.
Множества можно определять также при помощи операций над некоторыми другими множествами.
Пусть даны два множества: 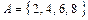 и
и 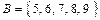 . Образуем множество
. Образуем множество 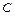 , в которое включим элементы, принадлежащие хотя бы одному из данных множеств, т.е. множеству
, в которое включим элементы, принадлежащие хотя бы одному из данных множеств, т.е. множеству  или множеству
или множеству  :
: 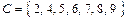 . Полученное множество
. Полученное множество 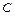 называют объединением множеств
называют объединением множеств  и
и  .
.
Определение. Объединением двух множеств  и
и  называется множество, состоящее из элементов, которые принадлежат хотя бы одному из этих множеств.
называется множество, состоящее из элементов, которые принадлежат хотя бы одному из этих множеств.
Объединение множеств  и
и  обозначают
обозначают 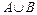 . Таким образом, по определению,
. Таким образом, по определению, 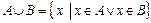 . Если изобразить множества
. Если изобразить множества  и
и  при помощи кругов Эйлера, то объединение данных множеств изобразится заштрихованной областью:
при помощи кругов Эйлера, то объединение данных множеств изобразится заштрихованной областью:
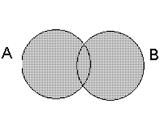
Если элементы множеств  и
и  перечислены, то, чтобы найти
перечислены, то, чтобы найти 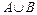 , достаточно перечислить элементы, которые принадлежат множеству
, достаточно перечислить элементы, которые принадлежат множеству  или множеству
или множеству  . Например:
. Например: 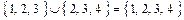 .
.
А как быть, если множества заданы характеристическими свойствами элементов? Из определения объединения следует, что характеристическое свойство элементов множества 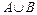 , составляется из характеристических свойств элементов множеств
, составляется из характеристических свойств элементов множеств  и
и  с помощью союза «или». Найдем, например, объединение множества
с помощью союза «или». Найдем, например, объединение множества  – четных натуральных чисел и множества
– четных натуральных чисел и множества  – двузначных чисел. Так как свойство элементов множества
– двузначных чисел. Так как свойство элементов множества  – «быть четным натуральным числом», а свойство элементов множества
– «быть четным натуральным числом», а свойство элементов множества  – «быть двухзначным числом», то в объединение данных множеств войдут числа, характеристическое свойство которых – «быть четным натуральным или двузначным числом». Такие числа образуют бесконечное множество, но сформулированное характеристическое свойство позволяет однозначно определять, содержится тот или иной элемент в объединении множеств
– «быть двухзначным числом», то в объединение данных множеств войдут числа, характеристическое свойство которых – «быть четным натуральным или двузначным числом». Такие числа образуют бесконечное множество, но сформулированное характеристическое свойство позволяет однозначно определять, содержится тот или иной элемент в объединении множеств  и
и  или не содержится. Например, в
или не содержится. Например, в 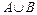 есть число
есть число  , поскольку оно четное; есть число
, поскольку оно четное; есть число 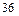 – оно четное и двузначное.
– оно четное и двузначное.
Рассмотрим теперь случай, когда находят объединение множества  и его подмножества
и его подмножества  . Легко видеть, что тогда
. Легко видеть, что тогда 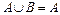 и, следовательно, характеристическое свойство элементов множества
и, следовательно, характеристическое свойство элементов множества 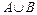 будет таким, как и свойство элементов множества
будет таким, как и свойство элементов множества  .
.
Умение вычленять множества в текстовых задачах и операций, которые над ними выполняются, - важный этап в их решений. Например, чтобы правильно выбрать действие, с помощью которого решается задача: «В букете 3 ромашки и 4 колокольчика. Сколько всего ‹цветков в букете?», надо понять, что в задаче рассматриваются два множества – множество ромашек в букете (в нем 3 элемента) и множество колокольчиков в этом букете (в нем 4 элемента); эти множества объединены в одно и требуется найти число элементов в этом объединении.
Пример:
1. Какие из следующих множеств геометрических фигур на плоскости равны между собой, если:  — множество всех квадратов;
— множество всех квадратов;  — множество всех прямоугольников;
— множество всех прямоугольников; 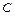 — множество всех четырехугольников с прямыми углами;
— множество всех четырехугольников с прямыми углами; 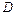 — множество всех прямоугольников с равными сторонами;
— множество всех прямоугольников с равными сторонами; 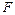 — множество всех ромбов с прямыми углами.
— множество всех ромбов с прямыми углами.
Ответ. Так как прямоугольник с равными сторонами и ромб с прямыми углами являются квадратами, то 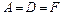 . Так как четырехугольник с прямыми углами является прямоугольником, то
. Так как четырехугольник с прямыми углами является прямоугольником, то 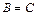 .
.
2. Для каждого из слов: «сосна», «осколок», «насос», «колос» составьте множество его различных букв. Имеются ли среди них равные?
Ответ.  = {с, о, н, а},
= {с, о, н, а},  = {о, с, к, л }, С={н, а, с, о}, D= {к, о, л, с}. Получили
= {о, с, к, л }, С={н, а, с, о}, D= {к, о, л, с}. Получили 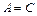 ,
, 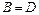 .
.
Пусть даны два множества: 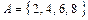 и
и 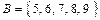 . Образуем множество
. Образуем множество 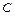 , в которое включим элементы, принадлежащие одновременно множеству
, в которое включим элементы, принадлежащие одновременно множеству  и множеству
и множеству  :
: 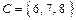 . Полученное множество
. Полученное множество 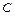 называют пересечением множеств
называют пересечением множеств  и
и  .
.
Определение. Пересечением двух множеств  и
и  называется множество, состоящее из элементов, которые одновременно принадлежат каждому из этих множеств.
называется множество, состоящее из элементов, которые одновременно принадлежат каждому из этих множеств.
Пересечение множеств  и
и  обозначают
обозначают 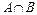 . Таким образом, по определению,
. Таким образом, по определению, 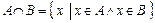 . Если изобразить множества
. Если изобразить множества  и
и  при помощи кругов Эйлера, то пересечение данных множеств изобразится заштрихованной областью:
при помощи кругов Эйлера, то пересечение данных множеств изобразится заштрихованной областью:
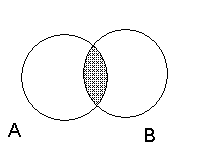
Если элементы множеств  и
и  перечислены, то, чтобы найти
перечислены, то, чтобы найти 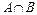 , достаточно перечислить элементы, которые принадлежат множествам
, достаточно перечислить элементы, которые принадлежат множествам  и
и  одновременно. Например:
одновременно. Например: 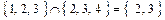 .
.
Пересечение множеств более сильная операция, чем объединение.
Если множества  и
и  не имеют общих элементов, то говорят, что эти множества не пересекаются, и обозначают:
не имеют общих элементов, то говорят, что эти множества не пересекаются, и обозначают: 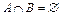 .
.
Если множества  и
и  имеют хотя бы один общий элемент, то говорят, что эти множества пересекаются, и обозначают:
имеют хотя бы один общий элемент, то говорят, что эти множества пересекаются, и обозначают: 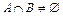 .
.
Если заданы два множества, то можно не только найти их пересечение и объединение, но и вычесть из одного множества другое. Результат вычитания называют разностью и определяют следующим образом.
Определение. Разностью множеств  и
и  называется множество, содержащее все элементы, которые принадлежат множеству
называется множество, содержащее все элементы, которые принадлежат множеству  и не принадлежат множеству
и не принадлежат множеству  .
.
Разность множеств  и
и  обозначают
обозначают 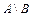 . Тогда, по определению, имеем:
. Тогда, по определению, имеем: 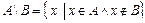 .
.
Если представить множества  и
и  при помощи кругов Эйлера, то разность
при помощи кругов Эйлера, то разность 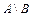 изобразится заштрихованной областью:
изобразится заштрихованной областью:
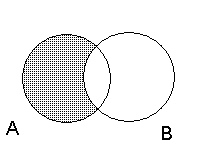
В школьном курсе математики чаще всего приходится выполнять вычитание множеств в случае, когда одно из них является подмножеством другого, при этом разность множеств 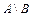 называют дополнением множества
называют дополнением множества  до множества
до множества  , и обозначают символом
, и обозначают символом 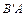 . Например:
. Например: 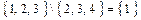 .
.
Определение. Пусть 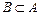 . Дополнением множества
. Дополнением множества  до множества
до множества  называется множество, содержащее все элементы множества
называется множество, содержащее все элементы множества  , которые не принадлежат множеству
, которые не принадлежат множеству  . Обозначается:
. Обозначается: 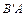 .
.
Из определения следует, что 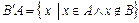 .
.
Как уже было сказано, в случае, когда 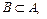 то
то 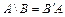 .
.
Выясним, как находить дополнение подмножества на конкретных примерах: Если элементы множеств  и
и  перечислены и
перечислены и 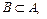 , то, чтобы найти дополнение множества
, то, чтобы найти дополнение множества  до множества
до множества  , достаточно перечислить элементы, принадлежащие множеству
, достаточно перечислить элементы, принадлежащие множеству  и не принадлежащие множеству
и не принадлежащие множеству  . Так, если
. Так, если 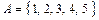 , а
, а 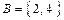 , то
, то 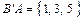 .
.
В том случае, когда указаны характеристические свойства элементов множеств  и
и  и известно, что
и известно, что 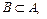 , то множество
, то множество 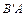 задают также с помощью характеристического свойства, общий вид которого
задают также с помощью характеристического свойства, общий вид которого 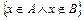 . Например, если
. Например, если  – множество четных чисел, а
– множество четных чисел, а  – множество чисел, кратных 4, то
– множество чисел, кратных 4, то 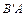 – это множество, содержащее такие четные числа, которые не делятся на 4. Например,
– это множество, содержащее такие четные числа, которые не делятся на 4. Например, 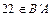 , так как
, так как 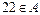 (т. е. оно четное) и
(т. е. оно четное) и 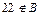 (т. е. оно не кратно 4).
(т. е. оно не кратно 4).
Каков порядок выполнения действий в выражении 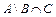 ? Условимся считать, что пересечение – более «сильная» операция, чем вычитание. Поэтому порядок выполнения действий в выражении
? Условимся считать, что пересечение – более «сильная» операция, чем вычитание. Поэтому порядок выполнения действий в выражении 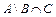 такой: сначала находят пересечение множеств
такой: сначала находят пересечение множеств  и
и 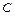 , а затем полученное множество вычитают из множества
, а затем полученное множество вычитают из множества  .
.
Что касается объединения и вычитания множеств, то их считают равноправными. Например, в выражении 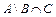 надо сначала выполнить вычитание (из
надо сначала выполнить вычитание (из  вычесть
вычесть  ), а затем полученное множество объединить с множеством
), а затем полученное множество объединить с множеством 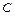 .
.
Задания для практических занятий и самостоятельного решения.
1. Изобразить на числовой прямой и записать в виде числовых промежутков множества 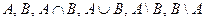 , если:
, если:
а) 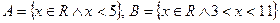 ; b)
; b) 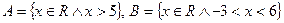 ;
;
c) 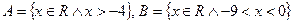 ; d)
; d) 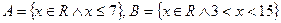 .
.
2. Известно, что 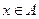 . Следует ли из этого, что
. Следует ли из этого, что 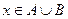 ?
?
3. Известно, что 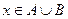 . Следует ли из этого, что
. Следует ли из этого, что 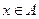 ?
?
4. Найдите объединение, пересечение и разность множеств  и
и  , если:
, если:
а) 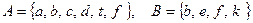 ; б)
; б) 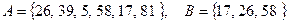 ;
;
в) 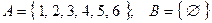 ; г)
; г) 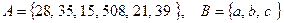 ;
;
д) 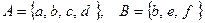 ; е)
; е) 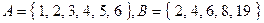 ;
;
ж) 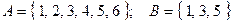 ; з)
; з) 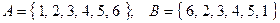 .
.
5. 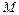 – множество однозначных чисел,
– множество однозначных чисел, 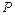 – множество нечетных натуральных чисел. Из каких чисел состоит объединение данных множеств? Содержатся ли в нем числа – 7 и 9?
– множество нечетных натуральных чисел. Из каких чисел состоит объединение данных множеств? Содержатся ли в нем числа – 7 и 9?
6. Требуется начертить две фигуры, принадлежащие пересечению множеств  и
и  , если:
, если:
а)  – множество ромбов,
– множество ромбов,  – множество прямоугольников;
– множество прямоугольников;
б)  – множество равнобедренных треугольников,
– множество равнобедренных треугольников,  – множество прямоугольных треугольников.
– множество прямоугольных треугольников.
Студент, выполняя задание а), начертил квадрат и прямоугольник со сторонами 2 см и 3 см., выполняя задание б), начертил равносторонний треугольник и прямоугольный треугольник с катетами 2 см и 3 см. Прав ли он?
7. Из каких элементов состоит объединение и пересечение множества букв в слове «математика» и множества букв в слове «геометрия»?
8. Известно, что 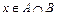 . Следует ли из этого, что а)
. Следует ли из этого, что а) 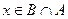 ; б)
; б) 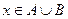 ?
?
9. Изобразить на диаграммах Эйлера – Вена следующие множества:
1) 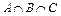 ; 2)
; 2) 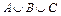 ; 3)
; 3) 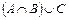 ; 4)
; 4) 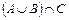 ; 5)
; 5) 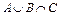 ; 6)
; 6) 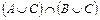 , 7)
, 7) 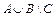 ; 8)
; 8) 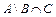 ; 9)
; 9)  ; 10)
; 10) 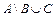 ; 11)
; 11) 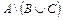 ; 12)
; 12) 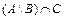 , 13)
, 13) 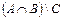 ; b)
; b) 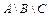 ; 14)
; 14) 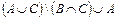 ; 15)
; 15) 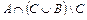 ;16)
;16) 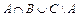 ; 17)
; 17) 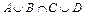 .
.
10. Найдите среди следующих выражений равные множества:
а) 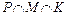 ; б)
; б) 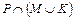 ); в)
); в) 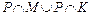 ; г)
; г) 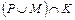 ; д)
; д) 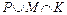 ; е)
; е) 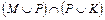 .
.
11. Даны множества:  – натуральных чисел, кратных
– натуральных чисел, кратных 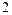 ,
,  –- натуральных чисел, кратных
–- натуральных чисел, кратных 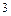 ;
; 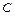 – натуральных чисел, кратных
– натуральных чисел, кратных 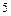 .
.
а) Изобразите на диаграмме Эйлера-Венна данные множества;
б) Сформулируйте характеристическое свойство элементов множеств 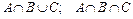 и назовите три элемента, которые им принадлежат.
и назовите три элемента, которые им принадлежат.
12. Даны множества:  - двухзначных чисел,
- двухзначных чисел,  - четных натуральных чисел,
- четных натуральных чисел, 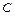 - натуральных чисел кратных 4.
- натуральных чисел кратных 4.
а) Изобразите множества  ,
,  и
и 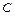 при помощи кругов Эйлера;
при помощи кругов Эйлера;
б) Укажите характеристическое свойство элементов каждого из множеств 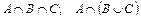 .
.
13. Известно, что 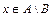 . Следуетли из этого, что: а)
. Следуетли из этого, что: а) 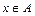 ; б)
; б) 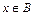 ?
?
14. Проиллюстрируйте при помощи кругов Эйлера, верны ли равенства для любых множеств  ,
,  и
и 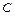 : а)
: а) 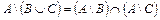 ; б)
; б) 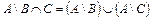 ;
;
в) 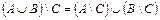 ; г)
; г) 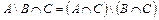 .
.
15.  – множество натуральных чисел, кратных 7,
– множество натуральных чисел, кратных 7,  – множество натуральных чисел, кратных 3,
– множество натуральных чисел, кратных 3, 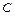 – множество натуральных четных чисел. Из каких чисел состоят множества:
– множество натуральных четных чисел. Из каких чисел состоят множества:
а) 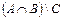 ; б)
; б) 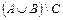 ; в)
; в) 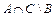 ; г)
; г) 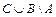 ?
?
 2015-05-22
2015-05-22 5466
5466







