2015-05-22
803
В автомашине 4 свободных места. Тогда три человека могут разместиться на них ____ различными способами.
| 24 | |
Решение:
В данном случае любое расположение 3 человек на 4 местах представляет собой упорядоченный набор из 3 элементов, выбранных из 4 элементов, то есть некоторое размещение. Так как все элементы набора различны, то речь идет о размещениях без повторений. Число размещений без повторений из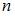 
по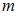 
элементов находится по формуле 
.
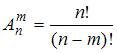В нашем случае необходимо найти число размещений без повторений из 4 по 3 элемента, то есть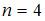 
, 
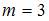. Следовательно, три человека могут разместиться на 4 местах 
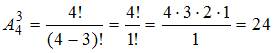способами.
Тема: Перестановки, размещения и сочетания
Количество всевозможных двузначных чисел, в которых цифры различны и отличны от нуля и единицы, равно …
| 56 | |
Решение:
В данном случае любая комбинация из 2 выбранных цифр представляет собой упорядоченный набор из 2 элементов, выбранных из 8 отличных от нуля и единицы цифр (2, 3, 4, 5, 6, 7, 8, 9), то есть некоторое размещение. Так как все цифры числа различны, то речь идет о размещениях без повторений. Число размещений без повторений из 
по элементов находится по формуле .
В нашем случае необходимо найти число размещений без повторений из 8 по 2 элемента, то есть , . Следовательно, искомое количество чисел равно .
|
|
|
