Во всех областях современной математики, за исключением узко специальных ее разделов, связанных с аксиоматическим построением теории множеств, понятие множества принято считать основным, неопределяемым понятием. Создатель теории множеств немецкий математик Г. Кантор (1845 – 1918) пояснил понятие множества следующим образом: «Множество, или совокупность - это собрание определенных и различных объектов нашей интуиции или интеллекта, мыслимое в качестве единого». Говорят также, что множество – это совокупность, собрание, или семейство каких-либо реально существующих или мыслимых объектов. Предполагается, что объекты, входящие в множество, попарно различны. Объекты, из которых составлено множество, называются его элементами.
Множества задаются двумя способами:
1) перечислением всех элементов множества;
2) указанием характеристического свойства элементов данного множества, т.е. такого свойства, которым обладают элементы данного множества и только они.
Введем необходимые обозначения и определения.
Множества обозначаются прописными латинскими буквами 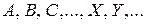 ; элементы множеств – строчными латинскими буквами
; элементы множеств – строчными латинскими буквами 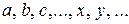 . Знак множества -
. Знак множества - 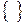 .
.
Например: а) 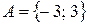 - конечное, двухэлементное множество.
- конечное, двухэлементное множество.
б) 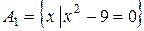 - множество
- множество 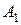 задано характеристическим свойством, т.е. это множество таких х, которые удовлетворяют уравнению
задано характеристическим свойством, т.е. это множество таких х, которые удовлетворяют уравнению 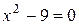 (т.е. множество корней уравнения
(т.е. множество корней уравнения 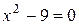 ).
).
На основании этого примера можно сделать вывод, что одно и тоже множество может быть задано разными характеристическими свойствами.
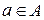 означает «элемент а принадлежит множеству А».
означает «элемент а принадлежит множеству А».
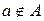 - «элемент а не принадлежит множеству А».
- «элемент а не принадлежит множеству А».
Множество, не содержащее ни одного элемента, называется пустым, и обозначается символом 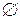 .
.
Два множества называются равными, если они состоят из одних и тех же элементов.
Так, в приведенном выше примере, множества 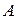 и
и 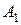 равные.
равные.
Для некоторых, часто используемых и известных из средней школы числовых множеств, существуют стандартные обозначения:
N = 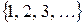 - множество целых неотрицательных чисел (или множество натуральных чисел), т.е. чисел, используемых при счете;
- множество целых неотрицательных чисел (или множество натуральных чисел), т.е. чисел, используемых при счете;
N0 = 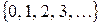 - множество целых неотрицательных чисел;
- множество целых неотрицательных чисел;
Z = 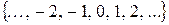 - множество целых чисел;
- множество целых чисел;
Q - 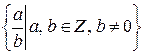 - множество рациональных чисел;
- множество рациональных чисел;
R – множество действительных чисел (или вещественных) чисел, т.е. чисел, представимых бесконечными десятичными периодическими дробями;
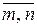 (для
(для 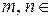 Z,
Z, 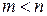 ) – множество
) – множество 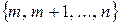 .
.
Если каждый элемент множества А является элементом множества В, то говорят, что А есть подмножество множества В (или В включает А), и пишут 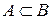 .
.
В частности, любое множество является подмножеством самого себя, т.е. 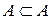 .
.
Пустое множество 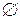 считается подмножеством любого множества А, т.е.
считается подмножеством любого множества А, т.е. 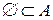 .
.
Очевидно, что множества 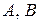 равны тогда и только тогда, когда
равны тогда и только тогда, когда 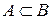 и
и 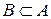 . Если
. Если 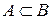 и
и 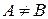 , то говорят, что
, то говорят, что 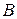 строго включает А, или А является собственным подмножеством множества В.
строго включает А, или А является собственным подмножеством множества В.
В повседневной практике нам часто приходится получать из одних множеств другие, например, объединяя заданные множества, выбирая из них общие или, наоборот, необщие элементы, и т.д. Для формализации таких способов получения множеств используются различные операции над множествами: пересечение, объединение, вычитание, дополнение и декартово произведение.
 2015-05-22
2015-05-22 1692
1692








