2015-05-22
1294
Пересечением множеств А, В называется множество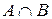 
, состоящее из всех тех элементов, которые содержатся в обоих множествах А, В: 
.
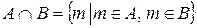Заметим, что пересечение двух множеств может оказаться пустым множеством. В этом случае исходные множества называются непересекающимися.
Пересечение множеств можно проиллюстрировать, используя, так называемые, круги Эйлера-Венна (здесь и далее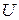 
– универсальное множество, т.е. множество, которое содержит в себе все слагаемые, перемножаемые и т.д. множества).
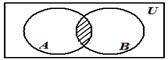
Рисунок 1
Из рисунка 1 видно, что пересечением множеств является их общая часть. Приведем примеры пересечения множеств:
1) 
, 
.
 |
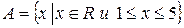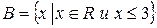С
Рисунок 2
Имеем,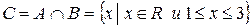 
.
2) А – множество треугольников на плоскости.
В – множество правильных многоугольников на плоскости.
Тогда 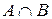- множество правильных треугольников на плоскости.
