Подмножество. Основные числовые множества

Опр. 2.1 Множество В, состоящее из некоторых элементов данного множества А (и только из них), называется подмножеством (частью) этого множества. Иначе, если любой элемент множества В принадлежит также множеству А, то множество В называется подмножеством множества А.

Это записывается так: ВÌ А или АÉВ. Говорят, что «В – подмножество А» или «В содержится в А» или «А содержит В». Заметим, что n (В) £ n (А).

Если все элементы множества А являются также элементами множества В, то говорят, что множество А включается (содержится) в множестве В.

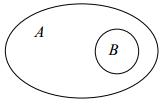
А Ì В

Если в множестве В найдется хотя бы один элемент, не принадлежащий множеству А, то В не является подмножеством множества А: ВËА. Например, отрезок [а, b] не является подмножеством полуинтервала (а, b], т.к. аÎ[а, b], но аÏ(а, b].

Из опр. 2.1 следует, что любое множество является подмножеством самого себя, т.е. справедливо утверждение АÌА. Полагают также, что пустое множество является подмножеством любого множества. Пустое множество не содержит ни одного элемента, а значит в нем нет элемента, не принадлежащего любому другому множеству.

Знак Ì называется знаком включения. Отметим основные свойства отношения включения между множествами:

1) ÆÌА для любого множества А;

2) АÌА для любого множества А (рефлексивность);

3) из того, что ВÌА не следует АÌВ (не симметричность);

4) если АÌВ и ВÌА, то А=В (антисимметричность);

5) если АÌВ и ВÌС, то АÌС (транзитивность).

Основные числовые множества:

N ={1,2,3,4,…} – множество натуральных чисел;

Z ={…,-4,-3,-2,-1,0,1,2,3,4,…} – множество целых чисел (содержит все натуральные числа и числа, им противоположные), NÌZ;

Q ={x ½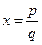, где pÎZ, qÎN } – множество рациональных чисел (состоит из чисел, допускающих представление в виде дроби), NÌZÌQ;

R =(-∞;+∞) – множество действительных чисел, QÌR (кроме всех рациональных чисел, содержит иррациональные числа, содержащие в своей записи знаки радикалов: ).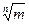

Действительные числа изображаются точками координатной прямой (числовой оси). Координатная прямая – это всякая прямая (обычно горизонтальная), на которой указаны положительное направление, начало отсчета и единичный отрезок.

Таблица 1. Правила изображения числовых промежутков.

Название	Неравенство, определяющее множество	Обозначение	Изображение
Отрезок от а до b (замкнутый промежуток)	а £ х £ b	[ a;b ]
Интервал от а до b	а < х < b	(a;b)
Полуинтервалы от а до b	а < х £ b а £ х < b	(a;b ] [ a;b)
Числовой луч от а до +∞	а £ х	[ a;+∞)
Открытый числовой луч от а до +∞	а < х	(a;+∞)
Числовой луч от -∞ до а	х £ а	(-∞; а ]
Открытый числовой луч от -∞ до а	х < а	(-∞; а)

Опр.2.2. Если А Í В, то множество А называется подмножеством множества В (также говорят, что В покрывает А). Если при этом А ¹ В, то множество А называется собственным подмножеством множества В и обозначается А Ì В.

Замечание. Не следует считать равносильными отношения принадлежности 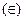и вхождения одного множества в другое 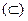. Можно привести следующий пример. Пусть А – множество всех студентов данной группы, а В – множество всех учебных групп данного института. Здесь 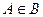, но 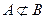, поскольку элементы этих множеств разнородны. Этот пример показывает также, что элементами множеств могут являться другие множества.

3. Операции над множествами.

После того, как мы научились составлять и различать множества, можно приступить к определению и других операций над ними. Естественно, что два множества могут иметь одинаковые элементы (их можно выделить в отдельное множество), из всех элементов двух множеств можно составить одно новое множество, также можно рассмотреть отдельно элементы одного множества, которых во втором множестве нет.

Например, А – множество наклеек (марок), которые есть у Пети, В – множество наклеек, которые собрал Вася. Можно выделить множество наклеек, которые есть у обоих ребят; коллекцию различных наклеек, собранных ими вместе; множество наклеек Пети, которых нет у Васи.

Таким образом, мы проделали операции пересечения, объединения и разности двух множеств.

Опр. 3.1 Пересечением множеств А и В называется множество С, состоящее из всех тех и только тех элементов, которые принадлежат каждому из данных множеств: С={х ½хÎА и хÎВ}. Обозначается, АÇВ.

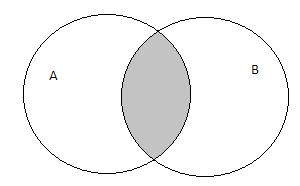
Опр. 3.2 Объединением множеств А и В называется множество С, которое состоит из всех элементов данных множеств А и В и только из них: С={х½ хÎА или хÎВ}. Обозначается, АÈВ.

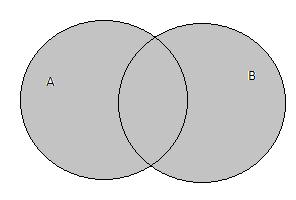
Геометрическое изображение множеств в виде области на плоскости называется диаграммой Эйлера – Вэйна.

Естественно поставить вопрос о нахождении числа элементов в объединенном множестве С. Если множества А и В не содержат одинаковых элементов, т.е. не пересекаются (АÇВ=Æ), то

n (АÈВ) = n (A) + n (B) (1).

В противном случае, когда множества имеют n (АÇВ) одинаковых элементов, следует пользоваться более общей формулой:

n (АÈВ) = n (A) + n (B) - n (АÇВ) (2).

Опр. 3.3 Разностью множеств А и В называется множество С, состоящее из всех элементов множества А, не принадлежащих множеству В: С={х ½ хÎА и хÏВ}. Обозначается, А\В.

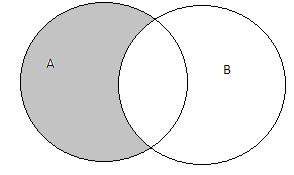
В случае, когда В является подмножеством А, т.е. ВÌА, разность А\В называется дополнением множества В до множества А (или относительно множества А).

В каждом отдельном случае мы рассматриваем (изучаем и пр.) всевозможные подмножества одного и того же множества. Например, в начальной школе дети учатся работать (выполнять основные арифметические операции) сначала с числами из первого десятка натуральных чисел, затем из первой сотни и т.д. Но их действия не выходят за рамки натуральных чисел (отрицательные и дробные числа они будут проходить позже). Аналогично, учитель может работать с некоторыми группами учеников, которые будут являться подмножествами определенного множества обучаемых данным учителем школьников. Каждый человек носит различные комбинации вещей, но только из своего личного гардероба. Это основное множество (свое в каждом отдельном случае) называется универсальным множеством.

Опр. 3.4 Универсальным множеством называется множество, подмножества которого (и только они) в данный момент рассматриваются. Обозначают, U.

При работе с числовыми множествами, если не дается дополнительных указаний, в качестве основного (универсального) множества будем считать множество R действительных чисел.

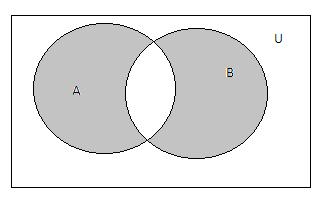
Опр. 3.5 Дополнением множества А называется разность U \А.. Обозначается, А’ или А и читается «не-А». Иначе, дополнением множества А называется множество А’, состоящее из всех элементов, не принадлежащих множеству А.

Симметрической разностью множеств A и B называется множество, состоящее из элементов исходных множеств, за исключением общих элементов.

Симметрическую разность множеств A и B обозначают A 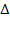B:

A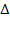B= (A\B)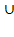(B\A).

Абсолютным дополнением множества A называется множество всех элементов, не принадлежащих A, т.е. множество `

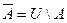, где U - универсальное множество.

Теперь укажем основные свойства изученных выше операций над множествами:

Свойства операции пересечения: 1) АÇА=А; 2) АÇÆ=Æ; 3) АÇА’=Æ; 4) АÇ U =А; 5) АÇВ=ВÇА.	Свойства операции объединения: 1) АÈА=А; 2) АÈÆ=А; 3) АÈА’= U; 4) АÈ U = U; 5) АÈВ=ВÈА.
Свойства операции разности: 1) А\А=Æ; 4) А\ U =Æ; 2) А\Æ=А; 5) U \А=А’; 3) А\А’=А; 6) Æ\А=Æ; 7) А\В ¹ В\А.

Справедливы равенства 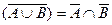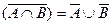(3).

Пример. Исходя из определения равенства множеств и операций над множествами, доказать тождество и проверить его с помощью диаграммы Эйлера - Вэйна.

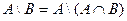
Из записанных выше соотношений видно, что

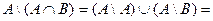Æ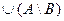= A \ В

Что и требовалось доказать.

Для иллюстрации полученного результата построим диаграммы Эйлера – Вэйна:

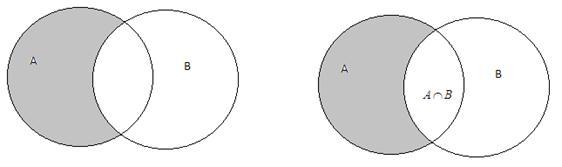
Пример. Исходя из определения равенства множеств и операций над множествами, доказать тождество.

A \ (B È C) = (A \ B) Ç (A \ C)

Если некоторый элемент х Î А \ (В È С), то это означает, что этот элемент принадлежит множеству А, но не принадлежит множествам В и С.

Множество А \ В представляет собой множество элементов множества А, не принадлежащих множеству В.

Множество А \ С представляет собой множество элементов множества А, не принадлежащих множеству С.

Множество (A \ B) Ç (A \ C) представляет собой множество элементов, которые принадлежат множеству А, но не принадлежат ни множеству В, ни множеству С.

Таким образом, тождество можно считать доказанным.

4. Разбиение множества на классы. Классификация

В процессе изучения предметов и явлений окружающего мира мы постоянно сталкиваемся с классификацией. Классификация широко используется в биологии, химии, математике, языке и многих других науках. Она облегчает процесс усвоения знаний.

Классификация в любой области человеческой деятельности связана с разбиением множества на подмножества (классы). Например, классификация частей речи, членов предложения, чисел, геометрических фигур и так далее.

Полученные подмножества должны обладать некоторыми свойствами:

1) они не должны быть пустыми;

2) не должны содержать общих элементов;

3) объединение всех подмножеств должно равняться самому множеству.

Определение: Классификацией или разбиением множества на классы называется представление этого множества в виде объединения непустых попарно непересекающихся своих подмножеств.

Для примера рассмотрим классификацию с помощью двух свойств.

Пусть U –множество студентов социально-педагогического факультета БГУ, свойство α - «быть отличником», свойство β - «быть спортсменом». С помощью указанных свойств можно выделить следующие подмножества:

А – множество отличников;

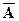– множество не отличников;

В – множество спортсменов;

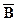– множество не спортсменов.

Множество U в этом случае оказывается разбитым на следующие четыре класса (подмножества):

II

I – множество отличников-спортсменов;

II – множество отличников - не спортсменов;

II

I

I – множество не отличников - спортсменов;

IV – множество не отличников - не спортсменов;

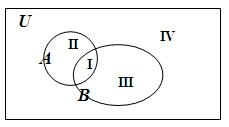
Рис. 2

Можно доказать, что если n – число свойств, то максимальное число классов в разбиении равно 2ⁿ.

Число элементов объединения и разности двух конечных множеств

Пусть A и B – конечные множества. Число элементов множества A условимся обозначать символом n ( A ) и называть численностью множества A.

Определим численность объединения множеств A и B.

Если множества A и B не пересекаются (см. рис. 1а), то n (A È B) = n(A) + n(B). Таким образом, численность объединения конечных непересекающихся множеств равна сумме численностей этих множеств.

Если множества A и B пересекаются (см. рис. 1б), то в сумме n(A) + n(B) число элементов пересечения A Ç B содержится дважды: один раз в n ( A ), а другой – в n ( B ). Поэтому, чтобы найти численность объединения n(A È B), нужно из указанной суммы вычесть n(A Ç B). Таким образом:

n(A È B) = n(A) + n(B) - n(A Ç B)

Определим теперь численность разности множеств A и B.

Если множества A и B не пересекаются, то A \ B = A, и поэтому n(A \ B) = n(A).

Если множества A и B пересекаются (см. рис. 1б), то n(A \ B) = n(A) - n(A Ç B).

Если В Ì А (см. рис. 1в), то A Ç B = B, и, следовательно, n(A \ B) = n(A) - n(B).