Для самостоятельного решения. 1. Найти вектор b, если 3(a1–2b)+5(a2+a3–3b)=2(a3–4b) и a1=(4,3,1,2), a2=(2,–1,–3,4), a3=(–1,4,–5,3)

1. Найти вектор b, если 3(a₁–2b)+5(a₂+a₃–3b)=2(a₃–4b) и a₁=(4,3,1,2), a₂=(2,–1,–3,4), a₃=(–1,4,–5,3).

2. Выясните линейную зависимость или независимость системы век­торов. Найдите какой-нибудь базис системы, укажите ее ранг. Выра­зите небазисные векторы через базисные:
а) (1,–1,1,–1), (1,0,1,0), (1,–3,1,–3);
б)(1,2,–1,0,3), (1,1,–1,3,–3), (2,3,2,–1,4), (1,5,–1,–9,21), (2,3,0,1,2);
в) (1,1,1,1,1), (1,2,3,4,1), (2,1,3,4,5), (1,2,–1,4,3).

3. Докажите, что при s>n любые s n-мерных векторов линейно за­висимы.

§3. Однородная система линейных уравнений.
Фундаментальный набор решений.

Общий вид О.С.Л.У. Нулевые и ненулевые решения О.С.Л.У. Доста­точное условие существования ненулевых решений. Определение фундамен­тального набора решений О.C.Л.У. Число решений, составляю­щих этот набор. План отыскания какого–нибудь ф.н.

Линейное уравнение называется однородным, если его свобод­ный член равен нулю. Система, состоящая из однородных уравнений, сама на­зывается однородной. Общий вид однородной системы m уравнений с n неизвестными есть:
а₁₁x₁+а₁₂x₂+…+а_1nx_n=0
а₂₁x₁+а₂₂x₂+…+а_2nx_n=0 (1)
…………………………
а_m1x₁+а_m2 x₂+…+а_mnx_n=0

Однородная система всегда совместна, так как x ₁=0, x ₂=0,…, x _n=0 одно из решений системы (1) называемое нулевым решением.

Во многих случаях важно знать, имеет ли данная однородная сис­тема еще и ненулевые решения.

Теорема 1. Однородная система, в которой число уравнений меньше числа неизвестных, всегда имеет ненулевые решения.

Теорема 2. Однородная система линейных уравнений имеет нену­левые решения тогда и только тогда, когда ранг матрицы, составленной из коэф­фициентов при неизвестных, меньше числа неизвестных.

Свойства решений однородной системы.

1. Если a – решение системы (1),то ka (где k – любое число) яв­ляется решением системы (1).

2. Если a и b – два решения системы (1), то a+b является ре­шением системы (1).

Теорема 3. Любая линейная комбинация решений однородной сис­темы есть снова решение этой системы.

Рассмотрим множество всех решений однородной системы (1). Это не­которое множество в n-мерном векторном пространстве V_{n .} Любой базис этого множества называется фундаментальным набором решений системы (1).

Иначе говоря, фундаментальный набор – это набор из конечного числа решений:

b₁,b₂,…_,b_p (2)
системы (1), удовлетворяющих условиям:

1. Вектора системы (2) линейно независимы;

2. Любое решение является линейной комбинацией векторов сис­темы (2).

Любые два фундаментальных набора состоят из одного и того же числа решений.

Теорема 4. Если b₁,b₂,…,b_p какой-либо фундаментальный набор реше­ний, то вектор g=k₁b₁+…+k_pb_p при всевозможных значениях парамет­ров k_1,k_2,…,k_p пробегает все решения системы (1) и поэтому является её общим ре­шением.

Рассмотрим способ построения фундаментального набора ре­шений. Для построения фундаментального набора воспользуемся методом Гаусса.

Применив его к системе (1), после ряда элементарных преобразо­ва­ний, прийдем к равносильной ей системе

с₁₁x₁+ с₁₂x₂+…+с_1,rx_r+с_1,r+1x_r+1+…+с_1nx_n=0
с₂₂x₂+…+с_2,rx_r+с_2,r+1x_r+1+… +с_2nx_n=0 (3)
…………………………………………….
c_r,rx_r+с_r,r+1x_r+1+… +с_rnx_n=0

или же к системе, получающейся из этой изменением нумерации неиз­вест­ных. Для определенности допустим, что получилась именно система (3). При­дадим свободным неизвестным в системе (3) следующие значения:
x _r+1=1, x _r+2=0, x _r+3=0,…, x _n=0,
после чего, найдем из системы значения остальных неизвестных x₁,x₂,…,x_r. Мы получим некоторое решение исходной системы (1) – обо­значим его a_r+1 (индекс _r+1 выбран в связи с тем, что при образовании этого решения неиз­вестное x _r+1 играет особую роль). Аналогичным обра­зом, полагая
x _r+1=0, x _r+2=1, x _r+3=0,…, x _n=0
и находя соответствующие значения x ₁, x ₂,…, x _r, получим еще одно реше­ние; обозначим его a_r+2. И так далее. Всего получим, таким образом, n–r реше­ний системы (1) a_r+1, a_r+2,...,a_n:

a_r+1=(l_r+1,1,l_r+1,2,…,l_r+1,r,1,0,0,…,0)
a_r+2=(l_r+2,1,l_r+2,2,…,l_r+2,r,0,1,0,…,0)
a_r+3=(l_r+3,1,l_r+3,2,…,l_r+3,r,0,0,1,…,0) (4)
……………………………
a_n=(l_n1, l_n2,…,l_nr, 0,0,0,…,1)

Векторы a_r+1,a_r+2,…,a_n образуют фундаментальный набор реше­ний.

Необходимо обратить внимание на следующий факт: число ре­шений в фундаментальном наборе равно n–r, т.e. разности между чис­лом неиз­вестных и рангом матрицы А, составленной из коэффициентов при неизвест­ных.

Задача 1. Найти какой-нибудь фундаментальный набор решений. Запи­сать на его основе все решения системы уравнений:

а) x₁+2x₂+4x₃ –3x₄ =0 б) 2x₁+3x₂ –2x₃ –5x₄ +x₅=0
3x₁+5x₂+6x₃ –4x₄ =0 4x₁+2x₂ +x₃ +2x₄ –3x₅=0
4x₁+5x₂ –2x₃ +3x₄ =0 –4x₂ +5x₃+12x₄–5x₅=0
3x₁+8x₂+24x₃–19x₄=0 – 6x₁ –x₂ –4x₃ –9x₄+7x₅=0

Решение. Рассматривая данные системы, как обычные системы ли­нейных уравнений, находим их решения. При этом выясняем наличие фун­даментального набора решений (ранг матрицы системы); определяем число решений, входящих в фундаментальный набор.

а) Применяем метод Гаусса:

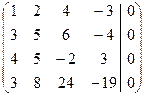
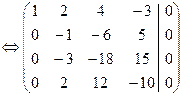
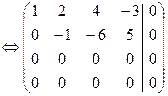
Из последней матрицы r_A=2. Так как число неизвестных больше ранга мат­рицы, то исходная система имеет фундаментальный набор решений, состоя­щий из n–r =4–2=2 решений. Из последней системы выразим глав­ные неиз­вестные через свободные:

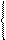x₁=–2x₂–4x₃+3x₄ x₁=8x₃–7x₄

x₂= –6x₃+5x₄ x₂=–6x₃+5x₄

Тогда фундаментальный набор, состоящий из двух решений, может быть выбран следующим образом:

X x1	x x2	xx3	xx4
	-–6
––7

Общее решение данной системы можно записать:

g=k₁b₁+k₂b₂,
где b₁=(8,–6,1,0); b₂=(–7,5,0,1); k₁,k₂ – произвольные числа.

б) Решаем систему методом Гаусса:
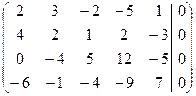
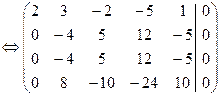
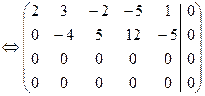, r_A=2.

Из последней системы выразим главные неизвестные через сво­бод­ные:
2x₁=–3x₂+2x₃+5x₄–x₅ x₁=–7/8×x₃–2x₄+11/8×x₅
x₂=5/4×x₃+3x₄–5/4×x₅, x₂=5/4×x₃+3x₄–5/4×x₅.

Фундаментальный набор состоит из n–r=5–2=3 решений и может быть выбран следующим образом:

x1	x2	X3	x4	x5
–7
–2
	–10

Общее решение системы можно записать:

w=l₁g₁+l₂g₂+l₃g₃, где g₁=(–7,10,8,0,0); g₂=(–2,3,0,1,0);
g₃=(11,­–10,0,0,8); l₁,l₂,l₃ –произвольные числа.
Ответ:

a) b₁=(8,–6,1,0); b₂=(–7,5,0,1) – фундаментальный набор; g=k₁b₁+k₂b₂
(k₁,k₂—произвольные числа) – все решения системы уравнений.

б) g₁=(–7,10,8,0,0); g₂=(–2,3,0,1,0); g₃=(11,–10,0,0,8) – фундаментальный набор; w= l₁g₁+l₂g₂+l₃g₃ (l_1,l₂,l₃ произвольные числа) – все решения системы уравнений.

Замечание. Всем свободным неизвестным можно придавать про­из­вольные значения. Но чтобы получить фундаментальный набор реше­ний надо заботиться о том, чтобы число частных решений было n–r (n–число не­известных системы, r–ранг матрицы системы), и чтобы эти решения были ли­нейно независимы.

Задача 2. Проверить образуют ли g₁=(2,2,0,4,1) и
g₂=(–1,0,2,–3,–2) фундаментальный набор решений системы уравнений:

3x₁ –2x₂+2x₃ –x₄ +2x₅=0
2x₁ +3x₂ –4x₃–2x₄ –2x₅=0
3x₁+2x₂ –x₃ –3x₄ +2x₅=0 (1)
x₁ –5x₂ +6x₃ +x₄+4x₄=0
6x₁ +x₃ –4x₄+4x₄=0

Решение. I способ. План решения: 1) убеждаемся в том, что g₁ и g₂ яв­ляются решениями системы (1); 2) если g₁ и g₂ – решения системы (1), то убеждаемся, что система векторов g₁ и g₂ линейно независима; 3) вычисляем ранг матрицы системы и оцениваем число решений, вхо­дящих в фундамен­тальный набор (оно должно быть равно 2). Проводим решение согласно этому плану;

1) непосредственно подставляем координаты g₁ в каждое уравне­ние системы:

3×2–2×2+2×0–1×4+2×1 =6–4–4+2 =0;
2×2+3×2–4×0–2×4–2×1 =4+6–8–2 =0;
3×2+2×2–1×0–3×4+2×1 =6+4–12+2=0;
1×2–5×2+6×0+1×4+4×1=2–10+4+4=0;
6×2 +1×0–4×4+4×1 =12–16+4 =0.

Cледовательно, g₁– решение системы (1). Аналогично убеждаемся, что
g₂ – решение системы (1).

2) вектора g₁ и g₂ – не пропорциональны, следовательно, система век­торов g₁ и g₂ – линейно независима;

3) вычисляем ранг матрицы системы:
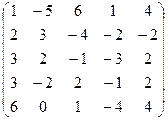
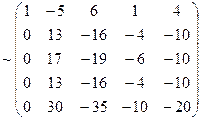
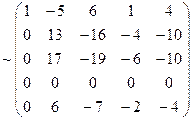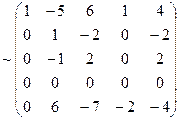
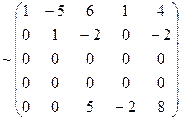
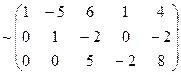~ , r_A=3
Тогда число решений фундаментального набора n–r=5–3=2.

Итак, на все пункты плана получили утвердительный ответ. По этому g_{1 и} g₂ образуют фундаментальный набор решений. Заметим, что если хотя бы на один пункт плана был получен отрицательный ответ, то g₁ и g₂ не образовывали бы фундаментального набора решений.

II cпособ. Находим обычным методом исключения неизвестных общее решение системы (1):
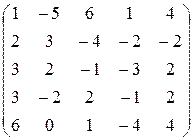
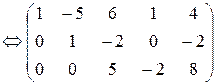, r_A=3.

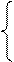
Свободных неизвестных два (х₄ и х₅). Выразим главные неизвест­ные через свободные:
x₁=5x₂–6x₃ –x₄ –4x₅; x₁=3/5×x₄–2/5×x₅;
x₂= 2x₃ +2x₅; x₂=4/5×x₄–6/5×x₅;
x₃= 2/5×x₄–8/5×x₅; x₃=2/5×x₄–8/5×x₅.

Фундаментальный набор состоит из n–r=5–3=2 решений. Найдём один из них. Положим сначала x ₄=4, x₅ =1 (четвертая и пятая координаты век­тора g₁), а затем x ₄=–3, x₅ =–2 (четвертая и пятая координаты вектора g₂). Получим частные решения:

x1	X2	x3	x4	x5
–1			–3	–2

это и есть вектора g₁ и g₂.

Таким образом, g₁ и g₂ являются решениями системы (1). Число за­данных решений g₁ и g₂ равно числу свободных неизвестных. Нако­нец, убе­ждаемся, что g₁ и g₂ линейно независимы. Следовательно, g₁ и g₂ составляют фундаментальный набор решений системы (1).

Задача 3. Решить систему линейных уравнений, используя связь ре­шений системы уравнений с решениями соответствующей системой одно­родных уравнений:
2x₁+3x₂ –2x₃ –5x₄ +x₅= –1
4x₁+2x₂ +x₃ +2x₄ –3x₅= 6
–4x₂+5x₃+12x₄ –5x₅= 8
–6x₁ –x₂ –4x₃ –9x₄+7x₅=–13

Решение. Замечаем, что если в данной системе заменить свобод­ные члены нулями, т. е. перейти к соответствующей однородной системе, то по­лучиться система из задачи 1. Нам известен ее фундаментальный набор реше­ний, а значит и обще решение: w= l₁g₁+l₂g₂+l₃g₃, где l₁,l₂,l₃ произвольные числа и g₁=(–7,10,8,0,0); g₂=(–2,3,0,1,0); g₃=(11,–10,0,0,8).

Так как сумма общего решения соответствующей однородной сис­темы и частного решения данной системы даст выражение для об­щего ре­шения данной системы, то найдем некоторое частное решение данной сис­темы.

Замечаем, что b=(1,1,1,1,1) удовлетворяет данной системе. Поэтому a= l₁g₁+l₂g₂+l₃g₃+b, где l₁,l₂,l₃ произвольные числа, есть общее решение дан­ной системы. Это же выражение можно расписать покоординатно
{(–7 l₁– 2 l₂+ 11 l₃+ 1, 10 l₁+ 3 l₂– 10 l₃+ 1, 8 l₁+ 1, l₂+ 1, 8 l₃+ 1) ÷ l₁,l₂,l₃ ÎR}

Ответ: {(–7 l₁– 2 l₂+ 11 l₃+ 1, 10 l₁+ 3 l₂– 10 l₃+ 1, 8 l₁+ 1, l₂+ 1, 8 l₃+ 1) ÷ l₁,l₂,l₃ ÎR}