а) Решим матричное уравнение АХ=Е, как пакет систем линейных уравнений:
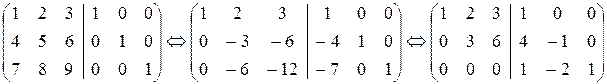
В любой из трех систем пакета третье уравнение противоречиво, т.e. матрица А не имеет обратной, а, значит, вырождена.
в) Решаем уравнение ВХ=Е, как пакет систем линейных уравнений:
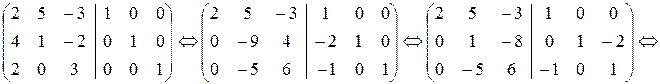


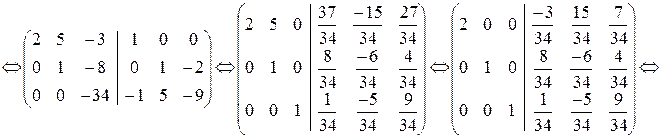
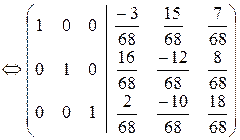
Тогда
X = 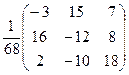
Проверка.
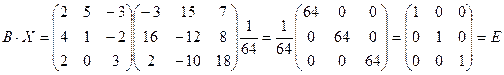
Значит, В –1= Х.
Замечание. Если для матрицы 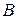 существует обратная (матрица
существует обратная (матрица 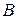 невырождена), то для нахождения
невырождена), то для нахождения 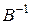 составляется комбинированная матрица
составляется комбинированная матрица 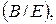 которая при помощи элементарных преобразований строк приводится к виду
которая при помощи элементарных преобразований строк приводится к виду 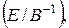 где справа от черты искомая матрица (способ элементарных преобразований строк).
где справа от черты искомая матрица (способ элементарных преобразований строк).
Ответ: а) для матрицы 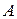 – обратной нет;
– обратной нет;
б) 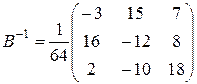
 2015-05-25
2015-05-25 690
690








