1. Перемножить матрицы. Определить, существуют ли оба произведения 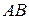 и
и 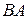 :
:
а) 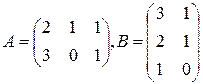 ; б)
; б) 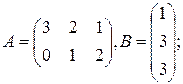
в) 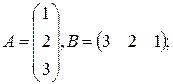 г)
г) 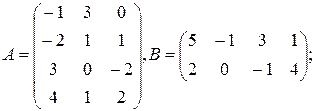
д) 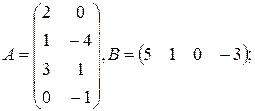
е) 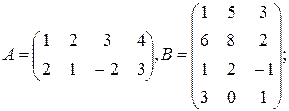
и) 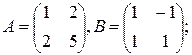 к)
к) 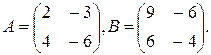
2. Вычислить 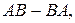 если:
если:
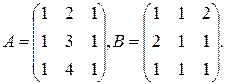
3. Найти значение многочлена от матриц:
a) 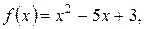
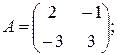
б) 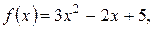
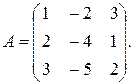
4. Найти матрицы, обратные данным:
a) 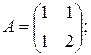 б)
б) 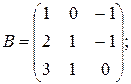 в)
в) 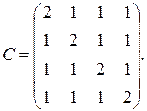
5. Решите матричное уравнение:
а) 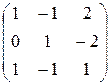 Х =
Х = 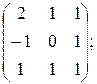 б)
б) 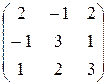 Х =
Х = 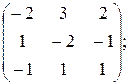
в) Х 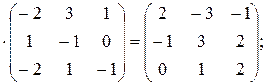
г) Х 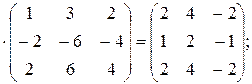
д) 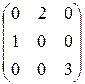 Х
Х 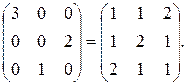
Указание. В уравнении 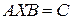 , обозначьте
, обозначьте 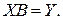
§5. Определитель квадратной матрицы.
Определитель второго и третьего порядков. Правило Саррюса. Свойства определителя. Миноры и алгебраические дополнения. Правило Крамера.
Пусть А – квадратная матрица n-го порядка над полем P:
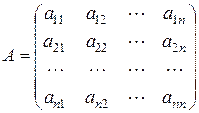
Определителем матрицы А n-го порядка называется алгебраическая сумма n! слагаемых, каждое из которых представляет собой произведение n элементов матрицы, взятых точно по одному из каждой строки и каждого столбца, со знаком «+», если перестановка от номеров столбцов чётная, и со знаком «–», если она нечётная. При этом в каждом произведении первый множитель – элемент первой строки, второй множитель – второй строки и.т.д.
Обозначают определитель матрицы А через | А |, det A, ∆ А,т.е.
| А |=det A =∆ А = 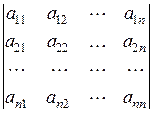
Итак,
| А |= 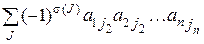 ,
,
где s(J) – число инверсий в перестановке (j1,j2,...,jn) номеров столбцов матрицы А: {1,2,3,...,n}. Символ J под знаком суммы указывает, что суммирование ведётся по всевозможным перестановкам множества {1,2,3,...,n} – номеров столбцов матрицы А.
Порядок матрицы называют и порядком её определителя. Данное выше определение позволяет получить формулы для вычисления определителей первого, второго, третьего порядков:
|A|= 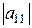 = a 11 . |A|=
= a 11 . |A|= 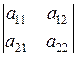 = a11a22–a12a21.
= a11a22–a12a21.
|A|= 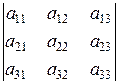 == a11a22a33+a12a23a31+a13a21a32–a13a22a31–a12a21a33–a11a23a32
== a11a22a33+a12a23a31+a13a21a32–a13a22a31–a12a21a33–a11a23a32
Для вычисления определителя третьего порядка обычно используют правило Саррюса: все слагаемые определителя и их знаки находятся по следующей схеме
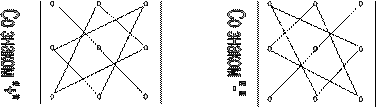 |
Определитель (n–1)-го порядка, полученный из определителя ∆А вычёркиванием i-той строки и j-го столбца, называется минором элемента aij и обозначается Мij. Алгебраическим дополнением Aij элемента aij называется минор Мij умноженный на (–1)i+j
Aij = (–1)i+j Мij.
Для вычисления определителей более высоких порядков используют следующие свойства определителей:
1. Определители квадратной матрицы А и транспонированной матрицы А T равны.
| А |= 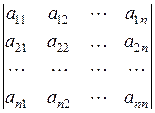 =
= 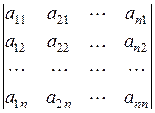 =| А T|
=| А T|
2. Определитель содержащий нулевую строку (нулевой столбец) равен нулю.
3. Перестановка двух строк (столбцов) определителя меняет его знак на противоположный.
4. Определитель, содержащий две одинаковые строки (два одинаковых столбца), равен нулю.
5. Общий множитель элементов любой строки (любого столбца) определителя можно выносить за знак определителя.
6. Если каждый элемент некоторой строки (некоторого столбца) представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, в каждом из которых все элементы те же, что и в исходном определителе, за исключением элементов указанной строки (указанного столбца). В первом определителе указанная строка (указанный столбец) состоит из первых слагаемых, во втором из вторых.
Например,
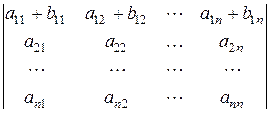 =
= 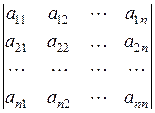
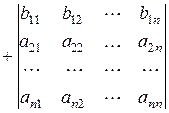
7. Определитель не изменится если к элементам некоторой строки (некоторого столбца) прибавить соответствующие элементы другой строки (другого столбца), умноженной (умноженного) на некоторое число.
8. Определитель можно разложить по строке либо столбцу по формулам:
| А |= ai1Ai1+ai2Ai2+…+ainAin (разложение по i-той строке), (1)
| А |=a1jA1j+a2jA2j+…+anjAnj (разложение по j-тому столбцу), (2)
т.е. определитель равен сумме произведений элементов некоторой строки (столбца) на их алгебраические дополнения.
9. Сумма произведений элементов какой-либо строки (какого-либо столбца) определителя на алгебраические дополнения соответствующих элементов другой строки (другого столбца) равна нулю.
ai1Aj1+ai2Aj2+…+ainAjn=0
10. Определитель матрицы равен нулю тогда и только тогда, когда вектора-строки (вектора-столбцы) матрицы линейно зависимы.
Между рангом произвольной матрицы любого порядка и её минорами существует связь: ранг ненулевой матрицы равен наибольшему из порядков ненулевых миноров.
Алгебраические дополнения используется для вычисления обратных матриц.
Теорема. Для квадратной матрицы А существует обратная матрица тогда и только тогда, когда определитель ∆ матрицы А отличен от нуля. Тогда обратная матрица вычисляется по формуле:
A –1= 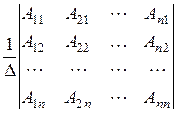

(здесь алгебраические дополнения строк матрицы А записываются в столбец).
Матрица
А *= 
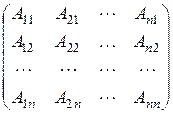
называется присоединённой для матрицы А.
Рассмотрим систему АХ=В (X, В – вектора-столбцы) n линейных уравнений с n неизвестными
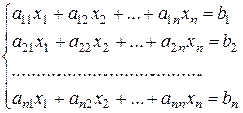 (3)
(3)
Теорема. Система (3) n линейных уравнений с n неизвестными является совместной определённой тогда и только тогда, когда определитель её основной матрицы ∆ отличен от нуля. В этом случае решения системы можно найти по формулам Крамера:
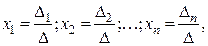
где определитель ∆i получается из определителя ∆ заменой i-го столбца на столбец свободных членов.
В качестве следствия получаем, что необходимым и достаточным условием наличия у однородной системы n линейных уравнений с n неизвестными ненулевых решений является равенство нулю определителя.
Решить систему (3) (если она совместна определена) можно с помощью обратной матрицы по формуле X=A–1B.
 2015-05-25
2015-05-25 622
622








