§4. Алгебра матриц.
Операции над матрицами. Обратная матрица. Матричное уравнение АХ=В. Система линейных уравнений как матричное уравнение.
Операции сложения, умножения транспонирования матриц, умножение матрицы на число. Матричное уравнение. Единичная матрица, обратная матрица. Вычисление обратной матрицы с помощью элементарных преобразований. Теоремы о ранге произведения матриц.
Пусть Р – некоторое поле (поле скаляров). Матрицы, составленные из элементов этого поля, будем называть матрицами порядка m  n, где m и n натуральные числа указывающие число строк и столбцов соответственно. Обозначать матрицу будем так:
n, где m и n натуральные числа указывающие число строк и столбцов соответственно. Обозначать матрицу будем так:
A= 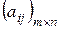 =
= 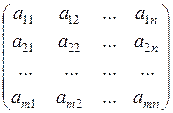
Если m=n то матрицу А называют квадратной матрицей порядка n. Обозначим i -ю строку матрицы А через А 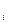 :
:
A 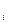 =
= 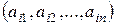 ,
,
а j -й столбец матрицы А – через Аj
A j= 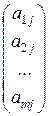
Две матрицы порядка 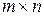
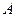 =
= 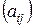 и
и 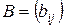 называют равными и пишут
называют равными и пишут 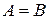 , если
, если 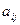 =
= 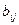 для любых наборов i,j где
для любых наборов i,j где 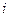 =1..n, j=1..m.
=1..n, j=1..m.
Матрица называется нулевой, если все ее элементы равны нулю.
Суммой двух матриц A и B порядка m 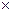 n называется матрица C порядка m
n называется матрица C порядка m 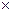 n, элемент
n, элемент 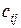 который равен
который равен 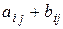 , т.e.
, т.e.
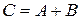 =
= 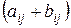 =
= 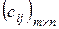
Произведением матрицы A = 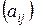 порядка
порядка 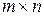 на число (скаляр)
на число (скаляр) 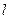
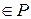 называется матрица D порядка
называется матрица D порядка 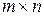 , элемент
, элемент 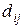 который равен
который равен 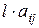 , т.e.
, т.e.
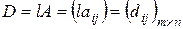
Нетрудно увидеть, что операции сложения матриц, умножения матрицы на скаляр обобщают аналогичные операции над арифметическими векторами (которые являются матрицами порядка 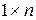 ) и обладают свойствами 1–8 (см §
) и обладают свойствами 1–8 (см § 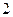 ).
).
Рассмотрим матрицу 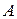 порядка
порядка 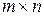 и матрицу
и матрицу 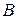
 порядка
порядка 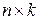 . Произведение строки
. Произведение строки 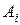 на столбец
на столбец 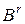 определим следующим образом:
определим следующим образом:
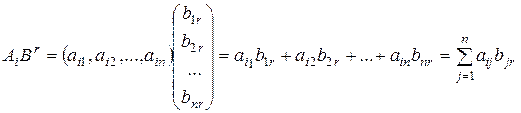
Произведением матриц 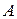 и B называется матрица
и B называется матрица 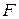 порядка
порядка 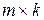 , такая, что,
, такая, что, 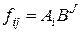 или
или
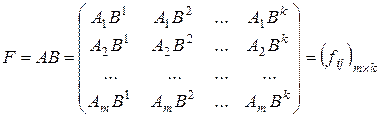
Согласно определению произведения матриц 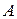 и
и 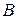 у матрицы
у матрицы 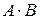 число строк совпадает с числом столбцов матрицы
число строк совпадает с числом столбцов матрицы 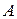 , а число столбцов – с числом столбцов матрицы
, а число столбцов – с числом столбцов матрицы 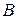 , т.e. если
, т.e. если 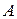 – матрица порядка
– матрица порядка 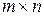 , а B – матрица порядка
, а B – матрица порядка 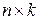 , то
, то 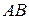 – матрица порядка
– матрица порядка 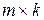 . При этом
. При этом 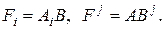
Непосредственный анализ определения операции умножения матриц показывает, что каждый столбец произведения матриц А и В линейно выражается через систему столбцов матрицы 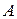 , а каждая строка этого произведения линейно выражается через систему срок матрицы
, а каждая строка этого произведения линейно выражается через систему срок матрицы 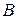 . Или более подробно:
. Или более подробно: 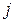 -ый столбец матрицы
-ый столбец матрицы 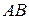 есть линейная комбинация всех столбцов матрицы
есть линейная комбинация всех столбцов матрицы 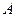 , коэффициенты этой комбинации – элементы
, коэффициенты этой комбинации – элементы 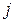 -го столбца матрицы
-го столбца матрицы 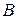 ,
, 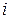 -ая строка матрицы AB есть линейная комбинация всех строк матрицы
-ая строка матрицы AB есть линейная комбинация всех строк матрицы 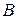 , а коэффициенты этой линейной комбинации – элементы
, а коэффициенты этой линейной комбинации – элементы 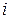 -ой строки матрицы
-ой строки матрицы 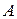 . Эти утверждения лежат в основе доказательства первой теоремы о ранге произведения матриц: ранг произведения матриц не превосходит ранга каждого из сомножителей:
. Эти утверждения лежат в основе доказательства первой теоремы о ранге произведения матриц: ранг произведения матриц не превосходит ранга каждого из сомножителей:
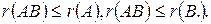
Умножение матриц не коммутативно, например:
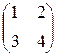
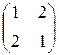 =
= 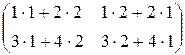 =
= 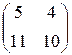
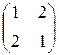
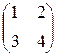 =
=  =
= 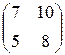
Если же 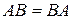 , то матрицы
, то матрицы 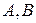 называют перестановочными.
называют перестановочными. 
Умножение матриц ассоциативно: если существуют произведения 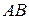 и
и 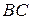 матриц, то существуют также и произведения
матриц, то существуют также и произведения 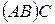 и
и 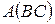 , и они равны:
, и они равны:
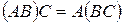 .
.
Отметим также, что
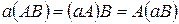
если произведение AB существует. Умножение матриц связано со сложением двумя дистрибутивными законами: если существуют матрицы A+B и AC то существуют также 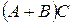 ,
, 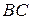 и
и
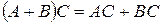
(правый дистрибутивный закон); если существуют 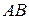 и
и 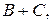 то существуют и
то существуют и 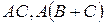 и
и
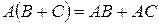
(левый дистрибутивный закон).
Транспонированием матрицы называют замену ее строк столбцами с сохранением порядка их записи, т.e. если 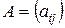 – матрица порядка
– матрица порядка 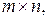 то транспонированная матрица
то транспонированная матрица 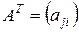 – порядка
– порядка 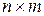 . Очевидно, что если
. Очевидно, что если 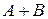 и
и 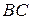 существуют, то существуют также
существуют, то существуют также 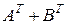 и
и 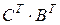 , и
, и
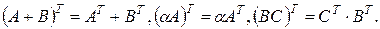
Рассмотрим систему 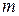 линейных уравнений с
линейных уравнений с 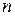 неизвестными:
неизвестными:
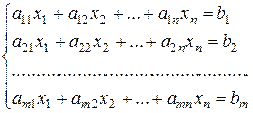 (1)
(1)
Обозначив через 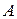 основную матрицу этой системы, через
основную матрицу этой системы, через 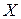 – одностолбцовую матрицу, составленную из неизвестных этой системы, а через
– одностолбцовую матрицу, составленную из неизвестных этой системы, а через 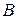 – одностолбцовую матрицу из ее свободных членов, запишем систему (1) в матричном виде:
– одностолбцовую матрицу из ее свободных членов, запишем систему (1) в матричном виде: 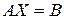 . Система линейных уравнений в матричной записи представляет собой частный случай матричных уравнений вида
. Система линейных уравнений в матричной записи представляет собой частный случай матричных уравнений вида
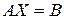 (2)
(2)
Уравнение вида ya=b сводятся к этому же типу матричных уравнений, поскольку (YA)T=BT и в результате A T Y T= B T.
Согласно определению умножения матриц, 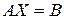 не имеет решений, если матрицы
не имеет решений, если матрицы 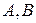 имеют различное число строк. Поэтому имеет смысл рассматривать уравнение вида (2), в которых число строк у матриц
имеют различное число строк. Поэтому имеет смысл рассматривать уравнение вида (2), в которых число строк у матриц 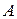 и
и 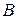 одно и то же.
одно и то же.
В равенстве 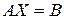 первый столбец матрицы
первый столбец матрицы 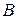 является произведением матрицы
является произведением матрицы 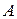 на первый столбец матрицы
на первый столбец матрицы 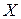 , второй столбец – произведением матрицы А на второй столбец матрицы
, второй столбец – произведением матрицы А на второй столбец матрицы 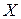 и т.д. Если
и т.д. Если 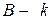 столбцовая матрица, то матричное уравнение
столбцовая матрица, то матричное уравнение 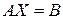 распадается на систему
распадается на систему 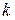 матричных уравнений:
матричных уравнений: 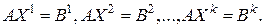 Каждое из этих матричных уравнений является системой линейных уравнений, причем все они имеют матрицу
Каждое из этих матричных уравнений является системой линейных уравнений, причем все они имеют матрицу 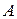 своей основной матрицей, и их решениями будут столбцы неизвестной матрицы
своей основной матрицей, и их решениями будут столбцы неизвестной матрицы 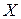 . Обычно, все эти линейные системы решаются одновременно, в виде пакета. Приведенные рассуждения позволяют, применив критерий Кроникера-Капелли, установить критерий разрешимости матричных уравнений: матичное уравнение
. Обычно, все эти линейные системы решаются одновременно, в виде пакета. Приведенные рассуждения позволяют, применив критерий Кроникера-Капелли, установить критерий разрешимости матричных уравнений: матичное уравнение 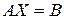 имеет решение тогда и только тогда, когда ранг матрицы
имеет решение тогда и только тогда, когда ранг матрицы 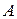 равен рангу матрицы ( А | В), т. e. матрицы полученной из матрицы
равен рангу матрицы ( А | В), т. e. матрицы полученной из матрицы 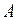 присоединением к ней матрицы
присоединением к ней матрицы 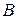 .
.
Квадратную матрицу, ранг которой равен ее порядку, называют невырожденной. Если ранг квадратной матрицы меньше ее порядка, матрицу называют вырожденной.
Заметим, что если в матричном уравнении 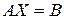 матрица
матрица 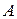 невырожденная, то это уравнение имеет единственное решение, так как каждая из систем линейных уравнений, на которые оно распадается, будет совместной и определенной.
невырожденная, то это уравнение имеет единственное решение, так как каждая из систем линейных уравнений, на которые оно распадается, будет совместной и определенной.
Квадратную 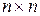 – матрицу вида:
– матрицу вида:
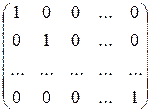
называют единичной и обозначают 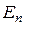 либо
либо 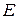 , если размеры известны или подразумеваются. Очевидно, что если
, если размеры известны или подразумеваются. Очевидно, что если 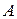 – квадратная
– квадратная 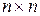 матрица, то
матрица, то 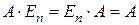 .
.
Если 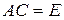 , то матрицу
, то матрицу 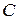 называют правой обратной для матрицы
называют правой обратной для матрицы 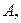 а матрицу A – левой обратной для матрицы C.
а матрицу A – левой обратной для матрицы C.
Видно, что матрица C является решением матричного уравнения 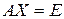 , причем, если A – невырожденная матрица, это решение единственное. Следовательно, всякая невырожденная матрица имеет единственную правую обратную матрицу. Обозначим правую обратную матрицу для матрицы A через
, причем, если A – невырожденная матрица, это решение единственное. Следовательно, всякая невырожденная матрица имеет единственную правую обратную матрицу. Обозначим правую обратную матрицу для матрицы A через 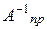 .
.
Ранг матрицы 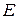 равен ее порядку, а если произведение матриц – матрица невырожденная, то согласно первой теореме о ранге произведения матриц, невырожденным будет и каждый сомножитель. Поэтому, если
равен ее порядку, а если произведение матриц – матрица невырожденная, то согласно первой теореме о ранге произведения матриц, невырожденным будет и каждый сомножитель. Поэтому, если 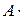
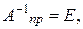 то
то 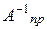 – тоже невырожденная и имеет для себя правую обратную. Пусть это будет матрица D, т. e.
– тоже невырожденная и имеет для себя правую обратную. Пусть это будет матрица D, т. e. 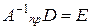 . Тогда с одной стороны
. Тогда с одной стороны 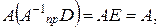 с другой –
с другой – 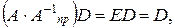 откуда вследствии ассоциативности умножения матриц
откуда вследствии ассоциативности умножения матриц 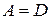 и
и 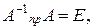 т. e. правая обратная матрица
т. e. правая обратная матрица 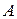 будет и ее левой обратной. Итак, всякая невырожденная матрица
будет и ее левой обратной. Итак, всякая невырожденная матрица 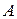 имеет единственную обратную двустороннюю матрицу, которую обозначают
имеет единственную обратную двустороннюю матрицу, которую обозначают 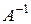 :
:
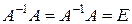 .
.
Одним из способов нахождения матрицы, обратной для матрицы 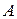 , является решение матричного уравнения
, является решение матричного уравнения 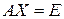 .
.
Согласно первой теореме о ранге произведения матриц, 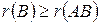 . Если матрица А невырожденная, то матрицу В можно записать в виде В=А–1×(АВ), и тогда (по той же теореме)
. Если матрица А невырожденная, то матрицу В можно записать в виде В=А–1×(АВ), и тогда (по той же теореме) 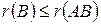 . Тем самым доказана вторая теорема о ранге произведения матриц: если матрица A невырожденная, то
. Тем самым доказана вторая теорема о ранге произведения матриц: если матрица A невырожденная, то 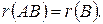
Задача 1. Вычислить 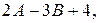 где
где
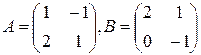
Решение. Так как в данное выражение вместо переменных подставляются матрицы, можно считать, что число 4 умножено на единичную матрицу, т. е. 4 надо понимать как 4 Е:
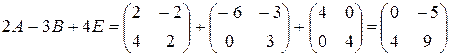 .
.
Ответ: 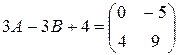 .
.
Задача 2. Вычислить AB, где
A = 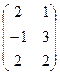 , B =
, B = 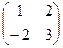 .
.
Решение. Число столбцов матрицы А равно числу строк матрицы B, значит произведение АВ существует (но ВА в этом случае не существует).
По определению произведения матриц для вычисления элемента cij матрицы С=АВ (т. е. элемента в i-й строке и j-м столбце), следует i-ю строку матрицы А умножить на j-й столбец матрицы В (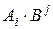 ). Например,
). Например,
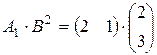 =
= 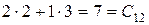 .
.
Запишем:
C = 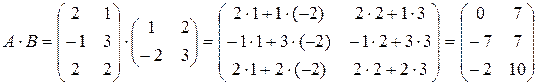 .
.
Ответ: C = 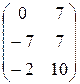 .
.
Задача 3. Вычислить АВ и ВА, если они существуют:
a) A = 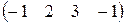 , B =
, B = 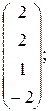
б) А = 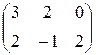 , B=
, B= 
в) А = 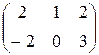 , В =
, В = 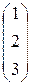
Решение.
а) А 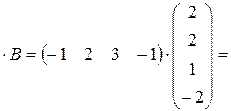 (–1
(–1 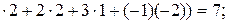
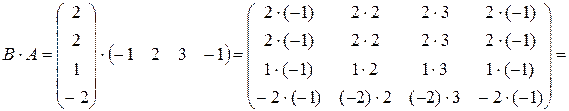
= 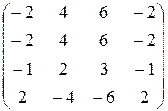 .
.
б) 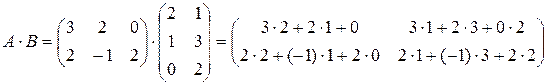 =
= 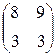 .
.
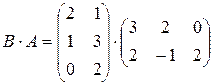 =
= 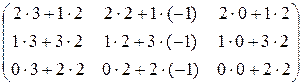 =
= 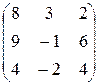 .
.
в) 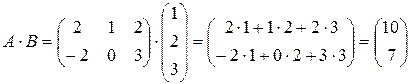 ,
,
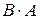 не существует.
не существует.
Ответ: a) 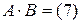 ,
, 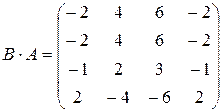 ;
;
б) 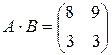 ,
, 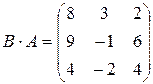 ;
;
в) 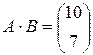 ,
, 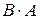 не существует.
не существует.
Задача 4. Вычислить f(A), если f(x)= x 2–2 x +1,
A = 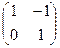
Решение.
f(A)= 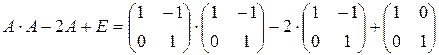 =
=
= 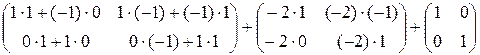 =
=
= 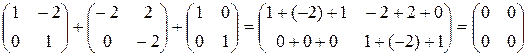
Ответ: f(A)= 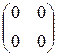 .
.
Задача 5. Решить матричное уравнение вида АХ=В.
а) 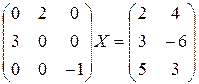 б)
б) 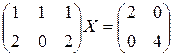
в) 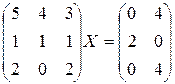 г)
г) 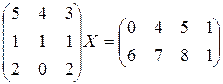
Решение. Матрица Х должна иметь столько строк, сколько столбцов у матрицы А, и столько столбцов, сколько столбцов у матрицы В. Для существования решения уравнения АХ=В необходимо, чтобы матрицы А и В имели одинаковое число строк. Поэтому в случае г) уравнение решения не имеет.
а) Матрица А – размера 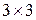 , матрица В – размера
, матрица В – размера 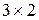 . Поэтому матрица Х размера –
. Поэтому матрица Х размера – 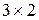 ,
,
Х = 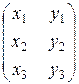
Тогда АХ=В можно записать так:
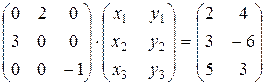 ;
;
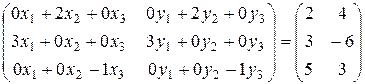 ;
;
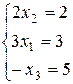 и
и 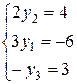 .
.
откуда
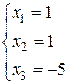 и
и 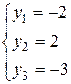 .
.
Итак X = 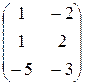 .
.
Проверка:
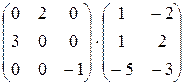 =
= 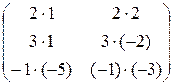 =
= 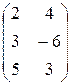 .
.
2 способ. Матричное равенство АС=В не измениться при одинаковых элементарных преобразованиях систем строк матриц А и В. Поэтому, при одинаковых элементарных преобразованиях систем строк матриц А и В уравнение АХ=В переходит в равносильное. Поменяем местами первую и вторую строки, затем первую строку умножим на (1/3), а вторую на (1/2), третью на (–1). Получим уравнение равносильное исходному:
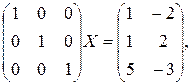 или Х =
или Х = 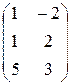 , т.к. Е =
, т.к. Е = 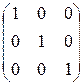 , ЕХ=Х.
, ЕХ=Х.
б) Матрица А – размера 3  3, матрица В – размера 3
3, матрица В – размера 3  2. Поэтому искомая матрица Х – размера 3
2. Поэтому искомая матрица Х – размера 3  2. Тогда исходное уравнение можно записать в виде:
2. Тогда исходное уравнение можно записать в виде:
A 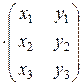 = B.
= B.
Это уравнение равносильно системе двух уравнений:
A 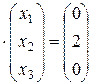 , A
, A 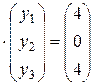 .
.
Каждое из этих уравнений является системой линейных уравнений с тремя неизвестными, причем у обеих систем одна и та основная матрица А. Поэтому их можно решать одновременно, написав столбцы свободных членов рядом.
Итак, матричное уравнение АХ=В есть пакет систем линейных уравнений с общей основной матрицей А:
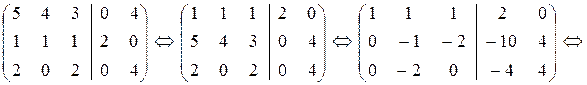
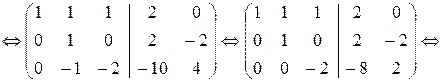
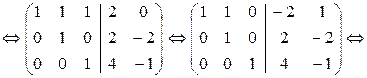
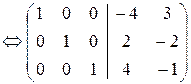 , т.е. Х =
, т.е. Х = 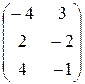 .
.
Фактически метод решения тот же, что и в пункте а), но элементарных преобразований больше, т.е. одними и теми же элементарными преобразованиями строк матриц А и В уравнение АХ=В было преобразовано в равносильное:
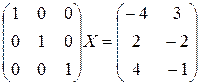 .
.
Проверка:
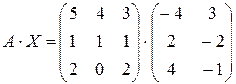 =
= 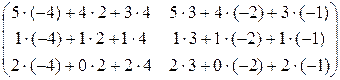 = =
= = 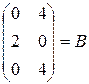 .
.
в) Решаем пакет двух систем линейных уравнений:
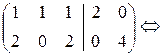
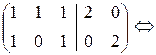
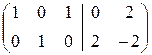 .
.
Замечаем, что обе системы, входящие в пакет, имеют бесконечно много решений при одном свободном неизвестном. Запишем их в виде:
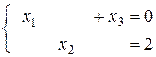 и
и 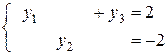 .
.
Значит
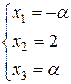 и
и 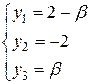 .
.
Поэтому
Х = 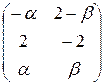 , где
, где 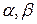 – любые числа.
– любые числа.
Проверка:
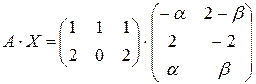 = =
= = 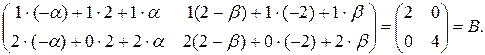
Ответ: a) X = 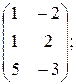 б) Х =
б) Х = 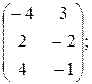
в) Х = 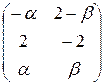 где
где 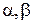 – любые числа; г) решений нет.
– любые числа; г) решений нет.
Задача 6. Решить матричное уравнение вида:
XA=B, если:
a) A = 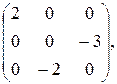 B =
B = 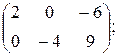
б) A = 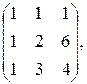 B =
B = 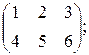
в) A = 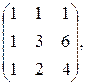 B =
B = 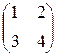
г) A = 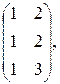 B =
B = 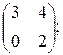
Решение. Для существования решения необходимо равенство числа столбцов матриц А и В. Поэтому в случае в) решения нет. На размеры матрицы Х влияет число строк матриц А и В: число строк матрицы Х равно числу строк матрицы В, число столбцов равно числу строк матрицы А.
а) Матрица В размера 2  3, матрица А размера 3
3, матрица А размера 3  3. Поэтому матрица Х размера 2
3. Поэтому матрица Х размера 2  3, т.е.
3, т.е.
Х = 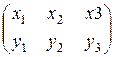 .
.
Тогда уравнение ХА=В запишется в виде:
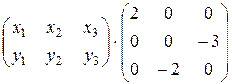 =
= 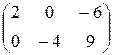
или 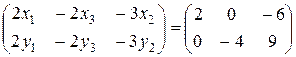 .
.
Откуда 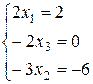 и
и 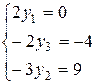 . Поэтому
. Поэтому 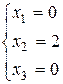 и
и 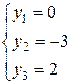 .
.
Тогда
X= 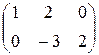 .
.
Проверка:
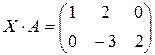
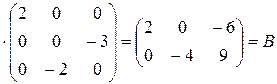 .
.
2 способ. Воспользуемся равенством 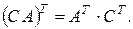 Тогда уравнение ХА=В перейдет в уравнение
Тогда уравнение ХА=В перейдет в уравнение 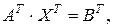 которое можно решить как пакет систем линейных уравнений, а затем решение транспонировать.
которое можно решить как пакет систем линейных уравнений, а затем решение транспонировать.
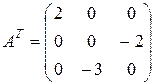
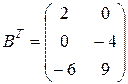
Решаем пакет двух систем уравнений:
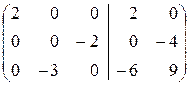 Û
Û 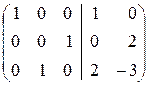 Û
Û 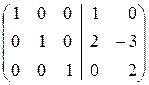
Тогда
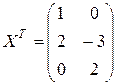 или
или 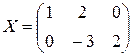 .
.
б) 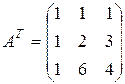 ,
, 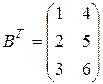 .
.
Решаем пакет систем уравнений:
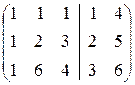 Û
Û 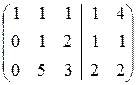 Û
Û 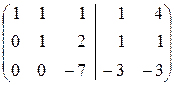 Û
Û
Û 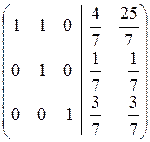 Û
Û 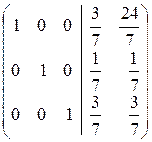 .
.
Тогда
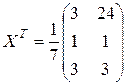 или
или 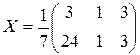 .
.
Проверка: 
XA= 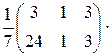
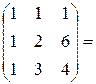
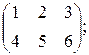 г) AT =
г) AT = 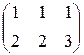 , B =
, B = 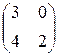 .
.
Решаем пакет двух систем уравнений:
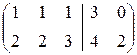 Û
Û 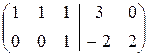 Û
Û 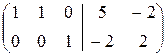
Откуда
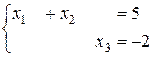 и
и 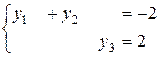 .
.
Системы являются совместными неопределёнными и имеют решения:
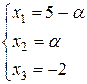 и
и 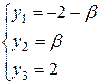 , где a,b ÎR.
, где a,b ÎR.
Тогда
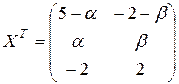 .
.
Поэтому
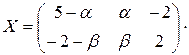
Проверка: 

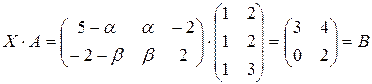
Ответ: а) Х = 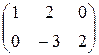 б) Х =
б) Х = 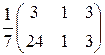
в) решения нет;
г) Х = 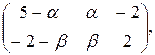 где
где 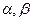 – любые числа,
– любые числа,
Задача 7 Вычислить матрицы обратные данным:
a) 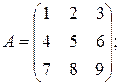 в)
в) 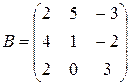
 2015-05-25
2015-05-25 3190
3190
