2015-06-10
1104
Пусть
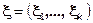
случайный вектор с совместной плотностью распределения
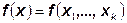
Из теоремы Фубини следует, что существует плотность распределения каждого подвектора
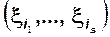
данного вектора, которая получается интегрированием совместной плотности по всем «свободным» переменным. В частности плотность i-той координаты вектора выглядит так
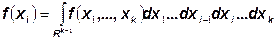
Плотность подвектора называется частная или маргинальная плотность.
Нетрудно показать, например, что маргинальные плотности многомерного нормального вектора также являются многомерными нормальными плотностями.
