Вычисление интеграла Лебега на прямой

Так как на распределение на прямой однозначно определяется функцией распределения

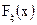
то интеграл Лебега часто обозначают так

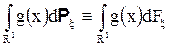
и называют интегралом Лебега-Стильтьеса от функции g по функции F.

Если функция распределения имеет плотность

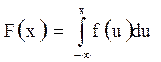
то предыдущий интеграл интеграл превращается в интеграл

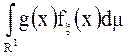
где

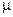
мера Лебега на прямой.

Для доказательства этого достаточно опять рассмотреть простые функции и перейти к пределу. Можно показать, что

если функция g (x) интегрируема по Риману, то

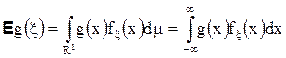
где последний интеграл понимается в смысле Римана.

Таким образом, в практически важных случаях вычисление интеграла Лебега сводится к вычислению конечной суммы, ряда или интеграла Римана (или их комбинаций). В дальнейшем для интегралов по мере Лебега будем опускать символ 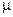и использовать такое же обозначение как и для интегралов Римана.