Доказательство. Для доказательства используем следующие две леммы

Для доказательства используем следующие две леммы.

Лемма 1.

Если 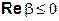, то

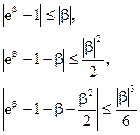
Доказательство леммы 1.

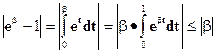
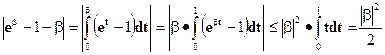
Третье неравенство доказывается аналогично.

Доказательство леммы 1 завершено.

Лемма 2.

Если 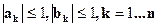, то

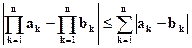
Доказательство леммы 2.

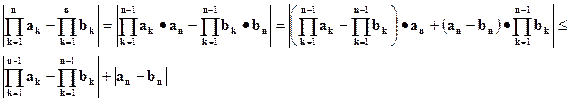Доказательство леммы 2 завершено.

Доказательство теоремы.

Используя леммы 1 и 2 и равенство

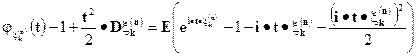
получаем

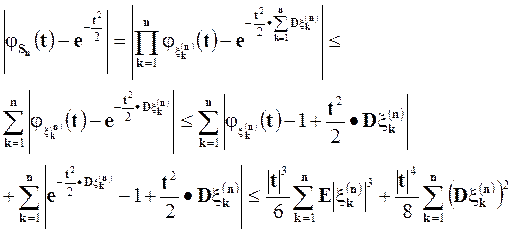Первая сумма стремится к нулю по условиям теоремы, а вторая потому, что

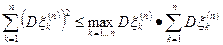
и по неравенству Ляпунова для моментов и условиям теоремы

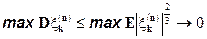
Теорема доказана.