Определение и основные свойства условного математического ожидания

Формальное определение условного математического ожидания является очень простым.

Пусть 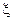- случайная величина с конечным математическим ожиданием, заданная на

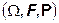
и 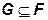- некоторая сигма-алгебра.

Случайная величина 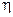называется условным математическим ожиданием случайной величины 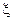относительно 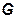, если

1. Случайная величина 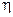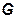- измерима

2. Для любого события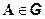

·

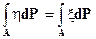
Условное математическое ожидание обозначается так

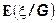
Напомним, что измеримость 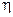относительно 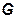означает, что

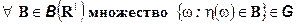
Заметим, что условие 2) в определении условного математического ожидания можно рассматривать как систему уравнений (количество уравнений равно количеству множеств в 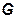, при заданной 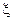правая часть к важдом уравнении известна) на функцию 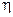, а условие 1) как описание класса функций, в котором ищется решение уравнения 2).

Прежде, чем исследовать вопросы существования и единственности условного математического ожидания в общей ситуации, приведем примеры вычисления условных математических ожиданий исходя из этого определения.