2015-06-10
1127
Многие свойства условного математического ожидания аналогичны и, в основном, доказываются аналогично соответствующим свойствам математического ожидания. В дальнейшем в этом пункте равенства и неравенства понимаются в смысле почти наверное и, при необходимости, предполагается существование у случайных величин математических ожиданий и вторых моментов.
1. 
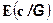= с
2. 
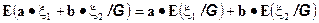
3. Если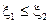 
, то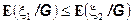 
4. 
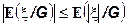
5. 
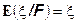
6. 
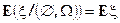
7. Если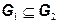 
, то
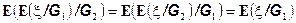
8. 
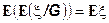
9. Пусть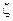 
- G – измерима, тогда
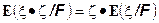
10. Пусть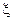 
не зависит от сигма-алгебры G, (т.е. любые события 
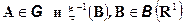независимы), тогда
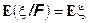
11. 
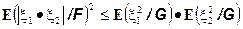-неравенство Коши -Буняковского
12. Если функция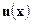 
выпукла как 
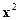, то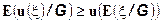 
-неравенство Йенсена
13. 
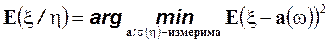
14. Для условных математических ожиданий верны теоремы о предельном переходе под знаком интеграла Лебега, в частности теорема о монотонной сходимости.
·
| Попробуйте доказать эти свойства. Самостоятельное доказательство поможет лучше понять определение условного математического ожидания | · Доказательства свойств 1)- 8) непосредственно следуют из определения условного математического ожидания, неравенства 11), 12) доказываются также как аналогичные неравенства для математического ожидания, свойства 9) и 10) сначала устанавливаются для простых функций, а затем переносятся на общий случай с помощью теорем о предельном переходе под знаком интеграла Лебега. Доказательство свойства 13) с учетом 6) и 9) аналогично доказательству соответствующего экстремального свойства математического ожидания. 14) получается применением теоремы для монотонной сходимости для интеграла Лебега. |
