Пусть 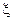 и
и 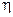 - случайные векторы произвольной конечной размерности (например, k и s) заданные на некотороми вероятностном пространстве
- случайные векторы произвольной конечной размерности (например, k и s) заданные на некотороми вероятностном пространстве
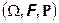
Функция 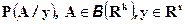 называется условным распределением случайной величины
называется условным распределением случайной величины 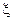 при условии
при условии 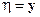 , если
, если
1. При каждом 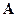 условная вероятность
условная вероятность 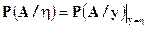
2. При каждом 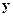 функция
функция 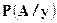 является распределением
является распределением
Замечательным является тот факт, что для любых случайных векторов условное распределение существует. Доказательство этого утверждения и более общие условия существования условного распределения можно найти, например, в книге Ширяева. Для условного распределения часто используют следующее обозначение:
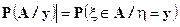
Если условное распределение при каждом 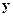 имеет плотность относительно некоторой меры
имеет плотность относительно некоторой меры 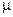 , то эта плотность называется условной плотностью распределения случайной величины
, то эта плотность называется условной плотностью распределения случайной величины 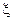 при условии
при условии 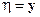 и обозначается
и обозначается
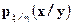
Обозначив 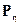 распределение случайной величины
распределение случайной величины 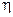 , используя свойства 8) и 9) условного математического ожидания получим, что для любых борелевских подмножеств
, используя свойства 8) и 9) условного математического ожидания получим, что для любых борелевских подмножеств 
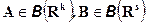
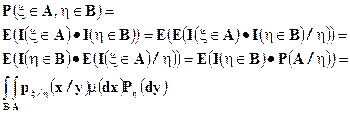
Наоборот, если функция 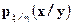 удовлетворяет соотношению
удовлетворяет соотношению
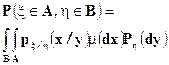
то она, очевидно, является условной плотностью.
Если распределение 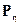 имеет плотность
имеет плотность 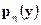 относительно меры
относительно меры 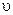 , то
, то
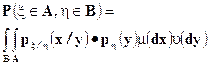
Данное соотношение означает, что функция
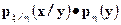
является совместной плотностью вектора 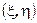 относительно произведения мер
относительно произведения мер 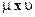
 2015-06-10
2015-06-10 339
339








