Теорема.
Если у вектора 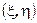 существует совместная плотность распределения
существует совместная плотность распределения 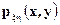 относительно произведения мер
относительно произведения мер 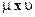 , то функция
, то функция
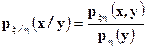
где
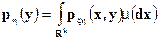
является условной плотностью распределения случайной величины 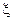 при условии
при условии 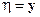
Доказательство.
Так как
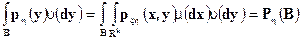 , то
, то 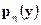 является плотностью распределения случайной величины
является плотностью распределения случайной величины 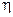 . Очевидно, также что
. Очевидно, также что
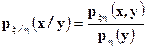
удовлетворяет условию
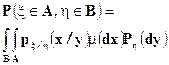 ,
,
эквивалентному определению условной плотности.
Доказательство завершено.
Через условную плотность легко выразить условное математическое ожидание
Теорема.
Пусть 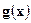 - борелевская функция из
- борелевская функция из 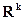 в
в 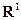 , тогда
, тогда
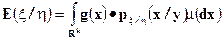
 2015-06-10
2015-06-10 311
311








