Доказательство. Рассмотрим вначале неотрицательную случайную величину

Рассмотрим вначале неотрицательную случайную величину 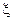. Определим функцию Q на сигма-алгебре 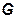следующим образом:

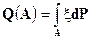
Используя свойства интеграла Лебега получаем, что функция Q неотрицательна, счетно-аддитивна по A и 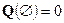. Следовательно это мера. Более того, эта мера абсолютно непрерывна (интеграл по множеству нулевой меры от любой случайной величины равен нулю) относительно сужения меры 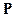на сигма-алгебру 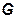и следовательно по теореме Радона-Никодима существует и единственна 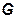- измеримая производная Радона-Никодима, удовлетворяющая условию:

для любого события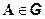

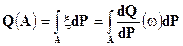
Ясно, что эта производная подходит под определение условного математического ожидания.

Для произвольных случайных величин поступим также, как при определении интеграла Лебега.