Если 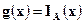 ,то теорема, очевидно, верна. Следовательно она верна для простых функций. Далее используем предельный переход под знаком интеграла Лебега.
,то теорема, очевидно, верна. Следовательно она верна для простых функций. Далее используем предельный переход под знаком интеграла Лебега.
Доказательство завершено.
Приведем пример вычисления условной плотности и условного математического ожидания.
Пример.
Пусть распределение вектора 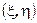 является двумерным нормальным распределением
является двумерным нормальным распределением
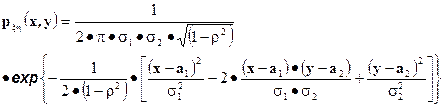
Тогда одномерная плотность 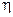 равна
равна
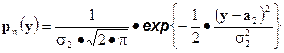
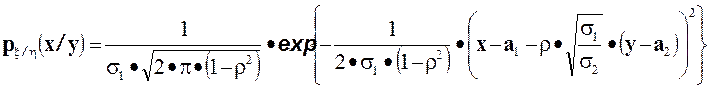 и условная плотность
и условная плотность
Замечая, что данная плотность является плотностью нормального распределения с математическим ожиданием 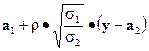
получаем, что
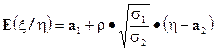
 2015-06-10
2015-06-10 273
273







