2015-06-10
756
Опр. Вероятностью события 
называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных, несовместных элементарных исходов, образующих полную группу.
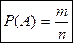, (2)
- где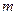 
- число исходов, благоприятствующих событию , 
- общее число элементарных исходов испытания.
Мы видим теперь, что подсчет вероятности в классической схеме сводится к подсчету числа «шансов» (элементарных исходов), благоприятствующих какому-либо событию, и общего числа шансов. Как правило, это делается с помощью формул комбинаторики. Но следует помнить, что три схемы: с возвращением и с учетом порядка, без возвращения и с учетом порядка, а также без возвращения и без учета порядка удовлетворяют классическому определению вероятности.
Четвертая же схема — схема выбора с возвращением и без учета порядка — имеет заведомо неравновозможные исходы и поэтому не удовлетворяет классическому определению вероятности.
1. 
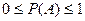. Вероятность случайного события есть положительное число, заключенное между 0 и 1.
¨ Случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае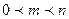 
, значит 
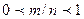и следовательно, 
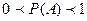. Итак, вероятность любого события . ¨
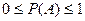2. 
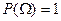. Вероятность достоверного события равна единице.
¨ Если событие достоверно, то каждый элементарный исход испытания благоприятствует событию. В этом случае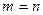 
, следовательно, 
. ¨
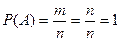3. 
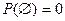. Вероятность невозможного события равна нулю.
¨ Если событие невозможно, то ни один из элементарных исходов испытания не благоприятствует событию. В этом случае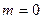 
, следовательно, 
. ¨
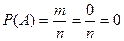4. Сумма вероятностей противоположных событий равна единице, т.е. если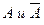 
- противоположные события, то 
.
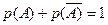¨ Противоположные события образуют полную группу, а сумма вероятностей событий, образующих полную группу, равна единице. ¨
