Недостатком классического определения вероятности является то, что оно неприменимо к испытаниям, число возможных исходов которых бесконечно. В таких случаях применяется метод, в котором по-прежнему основную роль играет понятие равновозможности некоторых событий. Применяется этот метод в задачах, сводящихся к случайному бросанию точки на конечный участок прямой, плоскости или пространства. Отсюда и возникает само название метода – геометрическая вероятность.
Суть метода состоит в следующем: если возможность случайного появления точки внутри некоторой области на прямой, плоскости или в пространстве определяется не положением этой области и ее границами, а только ее размером (длиной, площадью или объемом), то вероятность появления случайной точки внутри некоторой области определяется как отношение размера этой области к размеру всей области, в которой может появляться данная точка.
Так, для двумерного случая, вероятность попадания точки, брошенной наугад в область 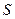 , в область
, в область 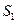 равна
равна
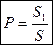 , (2)
, (2)
где 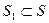 (рис. 2).
(рис. 2).
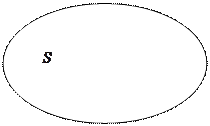
 |

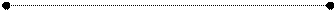
40 50 55 60 70
Рис.2 Рис.3
Пример 1. После бури на участке между 40-м и 70-м километрами телефонной линии произошел обрыв провода. Какова вероятность того, что разрыв произошел между 50-м и 55-м километрами линии?
¨ Пусть длина участка линии между 50-м и 55-м километрами равна единице, т.е. 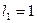 тогда длина всего участка (между 40-м и 70-м километрами) составляет шесть единиц, т.е.
тогда длина всего участка (между 40-м и 70-м километрами) составляет шесть единиц, т.е. 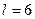 (рис.3). Используя формулу (2) для одномерного случая имеем:
(рис.3). Используя формулу (2) для одномерного случая имеем:
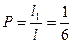 . ¨
. ¨
Пример 2. В круг радиуса R наудачу брошена точка. Найдите вероятность того, что эта точка окажется внутри данного вписанного правильного треугольника.
¨ Искомая вероятность равна отношению площади треугольника к площади круга:
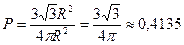 ¨
¨
Пример 3. Из отрезка 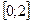 наудачу выбраны два числа
наудачу выбраны два числа  и
и 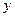 . Найти вероятность того, что эти числа удовлетворяют неравенствам
. Найти вероятность того, что эти числа удовлетворяют неравенствам 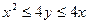 .
.
¨ По условиям опыта координаты точки 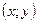 удовлетворяют системе неравенств:
удовлетворяют системе неравенств:
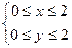 .
.
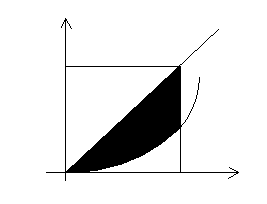
Это значит, что точка 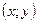 наудачу выбирается из множества точек квадрата со стороной 2 (рис.4). Интересующее нас событие происходит в том и только в том случае, когда выбранная точка
наудачу выбирается из множества точек квадрата со стороной 2 (рис.4). Интересующее нас событие происходит в том и только в том случае, когда выбранная точка 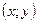 окажется в закрашенной фигуре. Эта фигура получена как множество точек, ординаты которых удовлетворяют неравенствам
окажется в закрашенной фигуре. Эта фигура получена как множество точек, ординаты которых удовлетворяют неравенствам 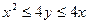 . Следовательно, искомая вероятность равна отношению площади закрашенной фигуры к площади квадрата:
. Следовательно, искомая вероятность равна отношению площади закрашенной фигуры к площади квадрата:
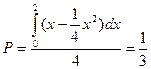 . ¨
. ¨
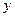
02 
Рис.4
Пример 4. Шар 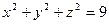 помещен внутри эллипсоида
помещен внутри эллипсоида 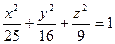 . Найти вероятность того, что поставленная наудачу внутри эллипсоида точка окажется внутри шара.
. Найти вероятность того, что поставленная наудачу внутри эллипсоида точка окажется внутри шара.
¨ Объем эллипсоида равен 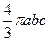 , где
, где 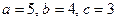 - полуоси эллипсоида; объем шара равен
- полуоси эллипсоида; объем шара равен 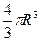 . Согласно формуле (9) для трехмерного случая имеем
. Согласно формуле (9) для трехмерного случая имеем
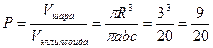 . ¨
. ¨
Пример5. (Задача о встрече.) Два человека  и
и  условились встретиться в определенном месте между двумя и тремя часами дня. Пришедший первым ждет второго в течение 10 минут, после чего уходит. Какова вероятность встречи этих лиц, если приход каждого из них в течение указанного часа может произойти в любое время?
условились встретиться в определенном месте между двумя и тремя часами дня. Пришедший первым ждет второго в течение 10 минут, после чего уходит. Какова вероятность встречи этих лиц, если приход каждого из них в течение указанного часа может произойти в любое время?
¨ Обозначим момент прихода одного человека через  , а второго через
, а второго через 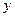 . Чтобы встреча состоялась, необходимо, чтобы
. Чтобы встреча состоялась, необходимо, чтобы
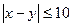 .
.
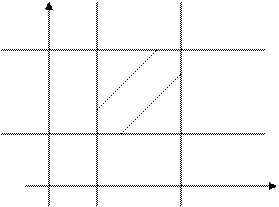
Будем рассматривать  и
и 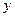 как декартовы координаты на плоскости; всевозможные исходы изобразятся точками квадрата со стороной
как декартовы координаты на плоскости; всевозможные исходы изобразятся точками квадрата со стороной 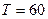 (минуты), а исходы, благоприятствующие встрече, располагаются в заштрихованной области (рис. 5). Время ожидания
(минуты), а исходы, благоприятствующие встрече, располагаются в заштрихованной области (рис. 5). Время ожидания 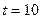 .
.
 часы
часы
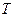
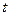
14 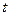
14  15 часы
15 часы
Рис. 5
Искомая вероятность равна отношению площади заштрихованной фигуры (полосы) к площади всего квадрата, т.е.
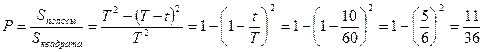 . ¨
. ¨
 2015-06-10
2015-06-10 7005
7005
