Опр. События  и
и  называются независимыми, если вероятность их совместного появления равна произведению вероятностей этих событий.
называются независимыми, если вероятность их совместного появления равна произведению вероятностей этих событий.
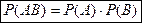 . (4)
. (4)
Опр. Событие  называется независимым по отношению к событию
называется независимым по отношению к событию  , если вероятность события
, если вероятность события  не зависит от того, произошло событие
не зависит от того, произошло событие  или нет. В противном случае событие
или нет. В противном случае событие  называется зависимым от события
называется зависимым от события  .
.
Опр. Если  и
и  - два зависимых события, то говорят об условной вероятности:
- два зависимых события, то говорят об условной вероятности:
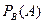 - вероятность события
- вероятность события  , при условии, что произошло событие
, при условии, что произошло событие  .
.
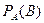 - вероятность события
- вероятность события  , при условии, что произошло событие
, при условии, что произошло событие  .
.
Опр. Условной вероятностью события  при условии, что произошло событие
при условии, что произошло событие  , называется число
, называется число
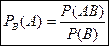 . (5)
. (5)
И условной вероятностью события  при условии, что произошло событие
при условии, что произошло событие  , называется число
, называется число
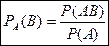 .
.
Введя понятие условной вероятности определение независимости событий можно сформулировать так:
Опр. Событие  называют независимым от события
называют независимым от события  , если появление события
, если появление события 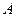 не изменяет вероятности события
не изменяет вероятности события  , т.е. если условная вероятность события
, т.е. если условная вероятность события  равна его безусловной вероятности:
равна его безусловной вероятности:
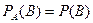 . (на основании (4) и (5))
. (на основании (4) и (5))
И что то же самое для события 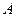 независимого от события
независимого от события  :
:
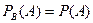 . (на основании (4) и (6))
. (на основании (4) и (6))
Лемма 2. Если события  и
и  независимы, то независимы и события
независимы, то независимы и события  и
и 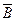 ,
, 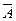 и
и  ,
, 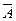 и
и 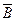 .
.
Опр. События 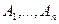 называются независимыми в совокупности, если для любого набора различных меж собой чисел
называются независимыми в совокупности, если для любого набора различных меж собой чисел 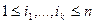 имеет место равенство
имеет место равенство
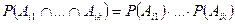 .
.
 2015-06-10
2015-06-10 650
650








