Задача. На плоскости начерчены параллельные прямые, находящиеся друг от друга на расстоянии 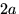 . На плоскость наудачу брошена игла длины
. На плоскость наудачу брошена игла длины 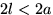 . Какова вероятность того, что игла пересечет одну из прямых?
. Какова вероятность того, что игла пересечет одну из прямых?
§ Поймем, что означает здесь «наудачу брошена игла». Возможные положения иглы (отрезка) на плоскости полностью определяются положением середины иглы и углом поворота иглы относительно какого-либо направления. Причем две эти переменные (положение центра и угол поворота) меняются независимо друг от друга.
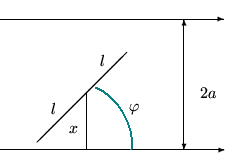
Обозначим через 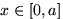 расстояние от середины иглы до ближайшей прямой, а через
расстояние от середины иглы до ближайшей прямой, а через 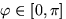 — угол между каким-то направлением прямых и иглой. Множество возможных положений иглы целиком определяется выбором наудачу точки из прямоугольника
— угол между каким-то направлением прямых и иглой. Множество возможных положений иглы целиком определяется выбором наудачу точки из прямоугольника 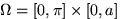 . Игла пересекает ближайшую прямую, если координаты выбранной наудачу точки удовлетворяют неравенству:
. Игла пересекает ближайшую прямую, если координаты выбранной наудачу точки удовлетворяют неравенству: 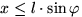 .
.
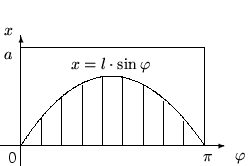
Площадь области 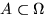 , точки которой удовлетворяют такому неравенству, равна
, точки которой удовлетворяют такому неравенству, равна
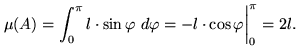
И так как 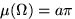 , то искомая вероятность равна
, то искомая вероятность равна
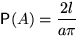 . §
. §
 2015-06-10
2015-06-10 5999
5999








