2015-06-10
14253
Пусть имеется полная группа несовместных гипотез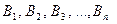 
. Известны вероятности каждой из гипотез: 
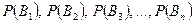. Производится опыт и в его результате осуществляется некоторое событие 
, вероятности которого по каждой гипотезе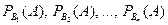 
(условные вероятности) известны. Вопрос: Какие вероятности имеют гипотезы 
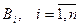в связи с появлением события ?
Т (формула Байеса: Thomas Bayes).
Условная вероятность того, что имело место событие 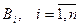, если в результате эксперимента наблюдалось событие , равна
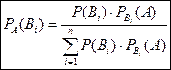. (1)
¨ По определению условной вероятности,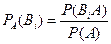 
, где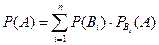 
- полная вероятность, а 
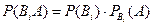, так как события зависимы. ¨
Замечание. Вероятности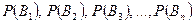 
часто называют априорными вероятностями группы гипотез 
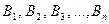, в то время как условные вероятности 
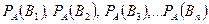– апостериорными, т.е. полученными после дополнительного эксперимента, в котором произошло событие . В связи с этим формула Байеса называется также формулой обновления априорных вероятностей.
Рассмотрим примеры на применение формулы гипотез.
Пример 9. В трех ящиках находятся однотипные изделия: в первом 10 изделий, из них 3 нестандартных, во втором 15 изделий, из них 5 нестандартных, в третьем 20 изделий, из них 6 нестандартных. Наудачу выбирается одно изделие, и оно оказалось нестандартное. Определить вероятность того, что взятое изделие принадлежало второму ящику.
¨ Введем обозначения гипотез:
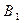- наудачу взятое изделие принадлежало первому ящику;
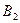- наудачу взятое изделие принадлежало второму ящику;
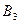- наудачу взятое изделие принадлежало третьему ящику.
В результате испытания наблюдается событие - наудачу выбранное изделие является нестандартным. Условные вероятности этого события при гипотезах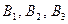 
соответственно равны:
, 
, 
.
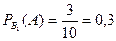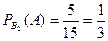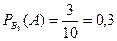По формуле (18) находим вероятность гипотезы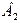 
после испытания:
. ¨
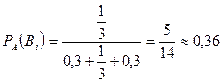Пример 10. В первой урне 2 белых и 6 черных шаров, во второй – 4 белых и 2 черных. Из первой урны наудачу переложили 2 шара во вторую, после чего из второй урны наудачу достали один шар. Требуется найти:
а) вероятность того, что этот шар белый.
б) Шар, взятый из второй урны, оказался белым. Какова вероятность того, что из первой урны во вторую были переложены 2 белых шара?
¨ а) Введем обозначения событий: А – шар, извлеченный из второй урны, белый; гипотезы: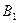 
– из первой урны во вторую переложены 2 белых шара, 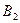– переложены 2 разноцветных шара, 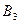– переложены 2 черных шара. Тогда по формуле (17)
,
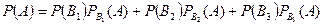где вероятности гипотез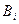 
и условные вероятности 
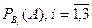вычисляем по классической схеме:
, 
, 
,
, 
, 
.
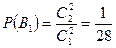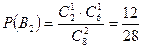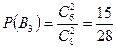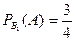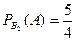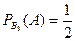Делаем расчет: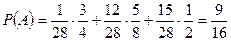 
.
б) Вероятность того, что шар оказался белым, находим по формуле Байеса:
.
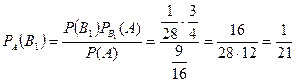Пример. Вероятность удовлетворять стандарту для изделий некоторого производства равна 0,9. Предлагается упрощенная схема проверки на стандартность, дающая положительный результат с вероятностью 0,95 для изделий, удовлетворяющих стандарту, и с вероятностью 0,15 для изделий, не удовлетворяющих стандарту. Найти вероятность того, что изделие, признанное при проверке стандартным, действительно удовлетворяет стандарту.
§ Обозначим: - «изделие будет признано при проверке стандартным», гипотезы: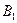 
- «изделие удовлетворяет стандарту», 
; 
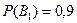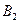- «изделие не удовлетворяет стандарту», 
.
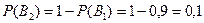По условию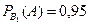 
, 
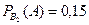. Требуется найти условную вероятность 
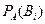. По формуле (1) получаем
.
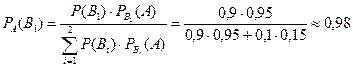Это означает, что на каждую сотню принятых деталей стандартных будет примерно 98.
