Т1. (сложение несовместных событий). Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий, т.е. если  и
и  - несовместные, то
- несовместные, то
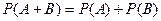 .
.
¨ Введем обозначения:  - общее число возможных элементарных исходов испытания;
- общее число возможных элементарных исходов испытания; 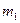 - число исходов, благоприятствующих событию А;
- число исходов, благоприятствующих событию А; 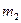 - число исходов, благоприятствующих событию В.
- число исходов, благоприятствующих событию В.
Число элементарных исходов, благоприятствующих наступлению либо события А, либо события В, равна 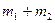 . Следовательно,
. Следовательно,
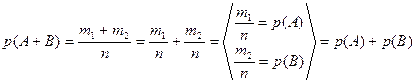 . ¨
. ¨
Следствие. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
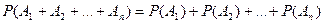 .
.
Т2. (сложение совместных событий). Вероятность появления одного из двух совместных событий равна сумме вероятностей этих событий, без вероятности их совместного появления, т.е. если  и
и  - совместные, то
- совместные, то
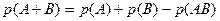 .
.
¨ Поскольку события  и
и  - совместные, то событие
- совместные, то событие 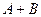 наступит, если наступит одно из следующих трех несовместных событий:
наступит, если наступит одно из следующих трех несовместных событий: 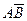 ,
, 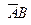 или
или 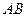 . По теореме сложения вероятностей несовместных событий,
. По теореме сложения вероятностей несовместных событий,
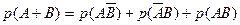 . (1)
. (1)
Событие  произойдет, если наступит одно из двух несовместных событий:
произойдет, если наступит одно из двух несовместных событий: 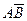 или
или 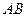 . По теореме сложения вероятностей несовместных событий имеем
. По теореме сложения вероятностей несовместных событий имеем
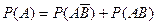 , Þ
, Þ 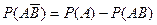 . (2)
. (2)
Аналогично имеем:
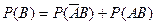 , Þ
, Þ 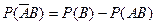 . (3)
. (3)
Подставив (2) и (3) в (1) получаем 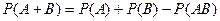 . ¨
. ¨
Замечания:
1. 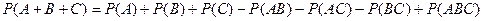 ;
;
2. Если 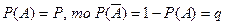 , т.е. вероятность противоположного события к событию
, т.е. вероятность противоположного события к событию  равна разности единицы и
равна разности единицы и 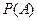 . ©
. ©
 2015-06-10
2015-06-10 848
848








