Рассмотрим урну, содержащую 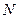 шаров, из которых
шаров, из которых 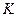 шаров — белые, а оставшиеся
шаров — белые, а оставшиеся 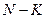 шаров — черные. Из урны наудачу (без возвращения) выбираются
шаров — черные. Из урны наудачу (без возвращения) выбираются  шаров. Вероятность того, что будет выбрано ровно
шаров. Вероятность того, что будет выбрано ровно 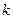 белых и
белых и 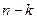 черных шаров, находится по формуле гипергеометрического распределения вероятностей:
черных шаров, находится по формуле гипергеометрического распределения вероятностей:
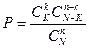
Если число шаров в урне очень велико, то извлечение одного, двух, трех шаров почти не меняет пропорцию белых и черных шаров в урне, так что вероятности 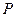 не очень отличаются от вероятностей в процедуре выбора с возвращением:
не очень отличаются от вероятностей в процедуре выбора с возвращением:
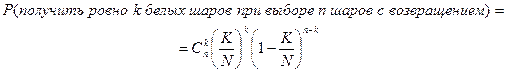
О. Говорят, что последовательности 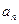 и
и 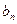 асимптотически эквивалентны, и пишут
асимптотически эквивалентны, и пишут 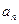 ~
~ 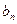 , если
, если 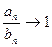 при
при 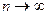 .
.
Свойство 1. Следующие последовательности асимптотически эквивалентны: 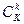 ~
~ 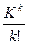 при
при 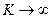 .
.
¨ Рассмотрим отношение членов этих последовательностей
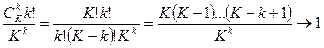 при
при 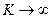 .
.
поскольку предел произведения конечного числа 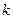 последовательностей, сходящихся к 1, равен 1. ¨
последовательностей, сходящихся к 1, равен 1. ¨
Следствие. 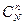 ~
~ 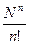 при
при 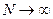 ,
, 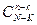 ~
~ 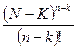 при
при 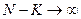 .
.
Сформулируем и докажем нашу первую предельную теорему.
Т1. Если 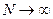 и
и 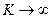 так, что
так, что 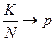 , то для любых фиксированных
, то для любых фиксированных  ,
, 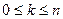
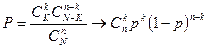
¨ Воспользуемся свойством 1 и следствием из него:
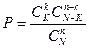 ~
~ 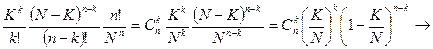
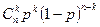 .
.
Мы получили, что 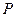 асимптотически эквивалентна выражению, сходящемуся к
асимптотически эквивалентна выражению, сходящемуся к 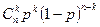 при
при 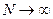 . Осталось вспомнить свойство:
. Осталось вспомнить свойство:
Свойство 2.
Пусть 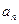 ~
~ 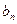 и существует
и существует 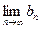 . Тогда существует и
. Тогда существует и 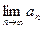 , и эти пределы совпадают:
, и эти пределы совпадают: 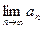 =
= 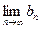 . ¨
. ¨
 2015-06-10
2015-06-10 680
680








