Вероятность 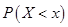 того, что случайная величина X окажется меньше некоторого вещественного числа
того, что случайная величина X окажется меньше некоторого вещественного числа 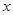 , называется функцией распределения случайной величины X, обозначается
, называется функцией распределения случайной величины X, обозначается 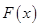 и определяется следующим образом:
и определяется следующим образом:
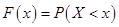
| (3.17) |
Свойства функции распределения:
1) 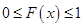 , т.к. это вероятность (по определению (3.18)).
, т.к. это вероятность (по определению (3.18)).
2) 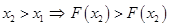 (
(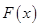 –неубывающая функция
–неубывающая функция 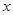 );
);
3) 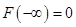 , т. к.
, т. к. 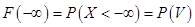 = 0.
= 0.
4) 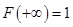 , т. к.
, т. к. 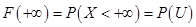 = 1.
= 1.
Напомним, 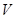 – невозможное событие,
– невозможное событие, 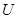 – достоверное событие.
– достоверное событие.
Пример 3.22
Построить функцию распределения для случайной величины 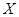 – числа выпадения гербов при двух бросаниях монеты.
– числа выпадения гербов при двух бросаниях монеты.
Решение
1) 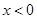 ,
, 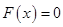 .
.
2) 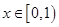 ,
, 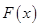 = 0,25.
= 0,25.
3) 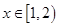 ,
, 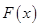 = 0,25 + 0,5 = 0,75.
= 0,25 + 0,5 = 0,75.
4) 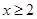
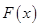 = 0,75 + 0,25 = 1.
= 0,75 + 0,25 = 1.
Отметим, что понятие функции распределения имеет место не только для дискретной, но и для непрерывной случайной величины.
 2015-06-10
2015-06-10 317
317








