В12.После дождя уровень воды в колодце может повыситься. Мальчик измеряет время падения t небольших камешков в колодец и рассчитывает расстояние от поверхности земли до уровня воды по формуле h = -5t². До дождя время падения камешков составляло 0,8 с. На какую наименьшую высоту должен подняться уровень воды после дождя, чтобы измеряемое время изменилось больше, чем на 0,1 с? (Ответ выразите в м.)
Решение:
Расстояние от поверхности земли до уровня воды мальчик рассчитывает по формуле
h = -5t². Обозначим время падения камешков до дождя t 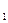 , после дождя t , после дождя t 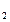 . По условию задачи t . По условию задачи t 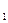 = 0,8 с; t = 0,8 с; t 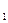 - t - t 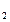 > 0,1; откуда t > 0,1; откуда t 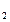 < t < t 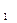 - 0,1.
Составим и решим неравенство: h ≤ -5 ((t - 0,1.
Составим и решим неравенство: h ≤ -5 ((t 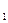 - 0,1) ²- t - 0,1) ²- t 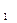 ²);
h ≤ -5 ((0,8 - 0,1) ²- 0,8²);
h ≤ -5 (0,7 ² - 0,8²);
h ≤ -5 (0,49 - 0,64);
h ≤ -5 · (-0,15);
h ≤ 0,75.
Значит, искомая наименьшая высота равна 0,75 м.
Другое решение:
До дождя уровень воды в колодце h ²);
h ≤ -5 ((0,8 - 0,1) ²- 0,8²);
h ≤ -5 (0,7 ² - 0,8²);
h ≤ -5 (0,49 - 0,64);
h ≤ -5 · (-0,15);
h ≤ 0,75.
Значит, искомая наименьшая высота равна 0,75 м.
Другое решение:
До дождя уровень воды в колодце h 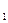 = -5∙0,8²= -5∙0,64.
После дождя уровень воды выше, значит, время падения камешков меньше на 0,1 с: h = -5∙0,8²= -5∙0,64.
После дождя уровень воды выше, значит, время падения камешков меньше на 0,1 с: h 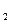 = -5∙(0,8-0,1)² = -5∙0,7 ²= -5∙0,49.
Тогда h = h = -5∙(0,8-0,1)² = -5∙0,7 ²= -5∙0,49.
Тогда h = h 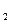 - h - h  = -5·0,49 - 5∙0,64 = -5 (0,49 – 0,64) = -5·(-0,15) = 0,75, т.е. искомая наименьшая высота равна 0,75 м.
В бланк ответов: 0,75 = -5·0,49 - 5∙0,64 = -5 (0,49 – 0,64) = -5·(-0,15) = 0,75, т.е. искомая наименьшая высота равна 0,75 м.
В бланк ответов: 0,75
|
Пример 6
|
|

Сейчас читают про:
 2015-06-10
2015-06-10 458
458







