а) Вычислительное устройство состоит из n независимо работающих элементов. Вероятность выхода из строя каждого элемента одинакова и равна p. Составить закон распределения случайной величины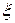 
- числа отказавших элементов. Построить график функции распределения 
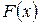. Найти 
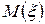и 
.
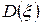| | n =2 | p =0,4 | | n =4 | p =0,1 |
| | n =3 | p =0,12 | | n =3 | p =0,15 |
| | n =4 | p =0,15 | | n =3 | p =0,2 |
| | n =2 | p =0,3 | | n =2 | p =0,2 |
| | n =2 | p =0,25 | | n =2 | p =0,1 |
| | n =3 | p =0,75 | | n =3 | p =0,1 |
| | n =3 | p =0,4 | | n =4 | p =0,5 |
| | n =4 | p =0,2 | | | |
б). При обработке деталей на станке автомате вероятность выхода размеров обрабатываемых деталей за границы «допуска» постоянна и равнее p. Для контроля качества отбирают n деталей. Построить график функции распределения 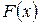случайной величины 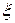- числа нестандартных деталей. Найт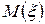и и 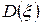. Определить наивероятнейшее число нестандартных изделий.
| | n =5 | p =0,1 | | n =3 | p =0,15 |
| | n =5 | p =0,15 | | n =3 | p =0,1 |
| | n =2 | p =0,2 | | n =2 | p =0,1 |
| | n =3 | p =0,25 | | n =2 | p =0,15 |
| | n =4 | p =0,15 | | n =4 | p =0,2 |
| | n =4 | p =0,1 | | n =6 | p =0,1 |
| | n =3 | p =0,2 | | n =5 | p =0,2 |
| | n =4 | p =0,2 | | | |
2015-06-10
1114
