2015-06-10
385
Совместные события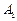 
, 
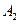с помощью противоположных 
, 
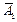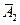могут быть представлены сумой следующих несовместных событий:
, 
,
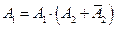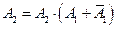или
, 
,
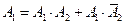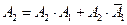что соответствует диаграмме Эйлера-Венна:
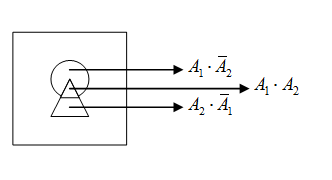
Тогда
,
,
.
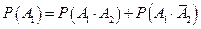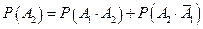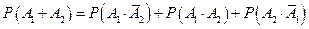Так как
,
,
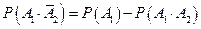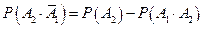то
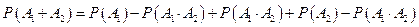
или
.
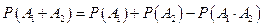Аналогичным методом находятся формулы вероятности суммы трех, четырех совместных событий
;
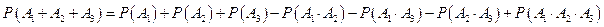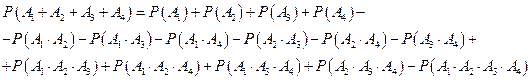
и далее методом математической индукции получим
.
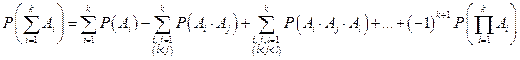3.6. Инвариантность (коммутативность) формулы вероятности произведения двух зависимых событий.
В соответствии с диаграммой Эйлера-Венна для совместных событий
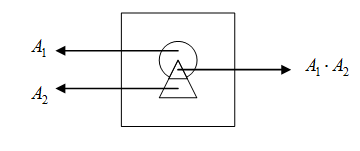
вводится так называемая условная (относительная) вероятность
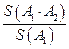или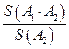 
,
обозначаемая в виде
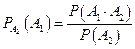или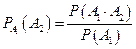 
,
которая определяется как отношение меры части геометрической формы (подмножества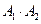 
) к мере всей формы (множества 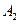или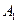 
), т.е. вероятность одного события при условии, что другое событие произошло (достоверно). Откуда следует симметричное (коммутативное) тождество:
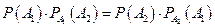
или
,
,
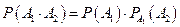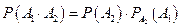что составляет содержание ранее приведенной теоремы об умножении вероятностей двух зависимых событий.
