Пример: Случайные события 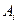
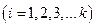 образуют полную группу несовместных событий (гипотез), вероятности которых
образуют полную группу несовместных событий (гипотез), вероятности которых 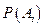 известны и связаны условием
известны и связаны условием 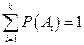 :
:
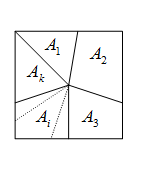
Событие А
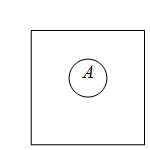
происходит совместно с одной из гипотез
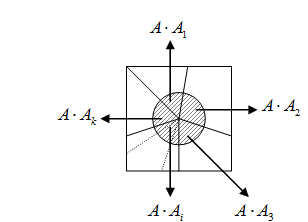
и условные вероятности 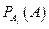 (вероятность события
(вероятность события 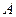 при каждой
при каждой 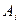 гипотезе) заданы. Найти вероятность события
гипотезе) заданы. Найти вероятность события 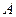 .
.
Решение: Из приведенной диаграммы следует
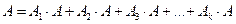 .
.
Откуда
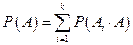 .
.
Используя условные вероятности, получим искомую формулу (формулу полной вероятности)
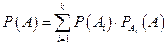 .
.
В силу симметричного (коммутативного) тождества, получим также
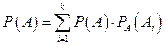 .
.
или
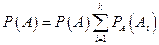 ,
,
т.е.
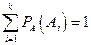 .
.
Итак, в результате осуществления (реализации) события 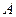 вероятности гипотез
вероятности гипотез 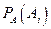 изменяются (перераспределяются), и также составляют полную группу несовместных событий.
изменяются (перераспределяются), и также составляют полную группу несовместных событий.
Пример: Работа двигателя контролируется двумя регуляторами. При наличии обоих регуляторов двигатель отказывает с вероятностью 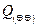 , при работе только первого из них − с вероятностью
, при работе только первого из них − с вероятностью 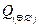 , при работе только второго − с вероятностью
, при работе только второго − с вероятностью 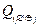 , при отказе обоих регуляторов −
, при отказе обоих регуляторов − 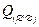 . Первый из регуляторов имеет надежность (вероятность безотказной работы)
. Первый из регуляторов имеет надежность (вероятность безотказной работы) 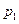 , второй −
, второй − 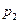 . Все элементы TS выходят из строя независимо друг от друга в течении заданного периода времени. Найти надежность TS.
. Все элементы TS выходят из строя независимо друг от друга в течении заданного периода времени. Найти надежность TS.
Решение:
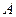 − безотказная работа TS (случайное событие),
− безотказная работа TS (случайное событие),
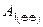 − работают оба регулятора (гипотеза),
− работают оба регулятора (гипотеза),
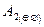 − работает первый регулятор, второй вышел из строя (гипотеза),
− работает первый регулятор, второй вышел из строя (гипотеза),
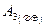 − работает второй регулятор, первый вышел из строя (гипотеза),
− работает второй регулятор, первый вышел из строя (гипотеза),
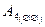 − оба регулятора отказали (гипотеза).
− оба регулятора отказали (гипотеза).
Найдем вероятности гипотез:
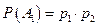 ,
,
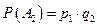 ,
,
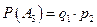 ,
,
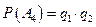 ,
,
где 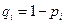 .
.
Условные вероятности события 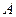 при этих гипотезах заданы:
при этих гипотезах заданы:
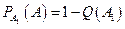 ,
,
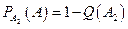 ,
,
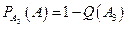 ,
,
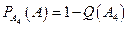 .
.
Таким образом, по формуле полной вероятности получим надежность TS:
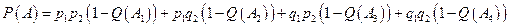 .
.
 2015-06-10
2015-06-10 745
745








