Пример: Случайные события 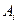
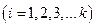 образуют полную группу несовместных событий (гипотез), вероятности которых
образуют полную группу несовместных событий (гипотез), вероятности которых 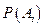 до испытания (эксперимента) известны и связаны условием
до испытания (эксперимента) известны и связаны условием 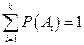 . Событие
. Событие 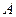 происходит совместно с одной из гипотез, причем условные вероятности
происходит совместно с одной из гипотез, причем условные вероятности 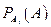 − известны. Произведен эксперимент, в результате которого наблюдается событие
− известны. Произведен эксперимент, в результате которого наблюдается событие 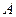 . Каким образом изменятся (перераспределятся) вероятности гипотез, когда результат испытания − событие
. Каким образом изменятся (перераспределятся) вероятности гипотез, когда результат испытания − событие 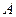 станет достоверным (появится, осуществится, реализуется), т.е. следует найти условные вероятности
станет достоверным (появится, осуществится, реализуется), т.е. следует найти условные вероятности 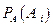 , связанные известным тождеством
, связанные известным тождеством 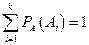 .
.
Решение: Используем ранее приведенное симметричное (коммутативное) тождество:
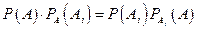
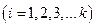 .
.
Откуда искомая условная вероятность находится
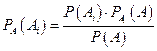 ,
,
где 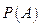 выражается известной формулой полной вероятности. Полученная формула условной вероятности называется формулой Бейеса (теорема гипотез).
выражается известной формулой полной вероятности. Полученная формула условной вероятности называется формулой Бейеса (теорема гипотез).
Пример: Узел (подсистема TS) собирается из качественных деталей (элементов) и деталей, имеющих дефекты. Известно, что 40% узлов собирается из качественных деталей. Если узел собран из качественных деталей, его надежность (вероятность безотказной работы) за установленное время равна 0,95; если из дефектных деталей − его надежность равна 0,7. Узел испытывался в течении установленного времени и работал безотказно. Найти вероятность того, что узел собран из качественных деталей.
Решение: Строятся гипотезы:
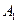 − узел собран из качественных деталей;
− узел собран из качественных деталей;
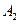 − узел собран из дефектных деталей.
− узел собран из дефектных деталей.
До испытания вероятность этих гипотез известна:
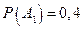 ,
,
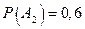 .
.
Известна также вероятность безотказной работы узла 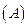 при гипотезах
при гипотезах 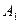 и
и 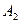 , т.е.
, т.е.
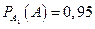 ,
,
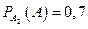 .
.
После испытания оказалось − узел безотказно работал установленное время 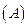 . Тогда условные вероятности гипотез (после эксперимента) найдем по формуле Бейеса:
. Тогда условные вероятности гипотез (после эксперимента) найдем по формуле Бейеса:
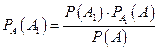 ,
, 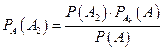 ,
,
где
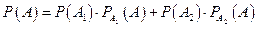 ,
,
т.е.
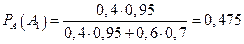 ,
, 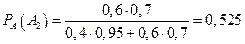 .
.
Критерий проверки: 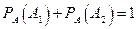 .
.
Действительно: 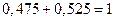 .
.
 2015-06-10
2015-06-10 574
574








