2015-06-04
860
Рассмотрим состояние равновесия жидкости в общем случае, т.е. когда на неё действует сила тяжести и сила инерции переносного движения при относительном покое.
Выделим в покоящейся жидкости элементарный объем в форме прямоугольного параллелепипеда с ребрами, параллельными координатным осям и соответственно равным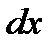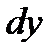и 
, 
и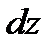 
(рис. 2.6).
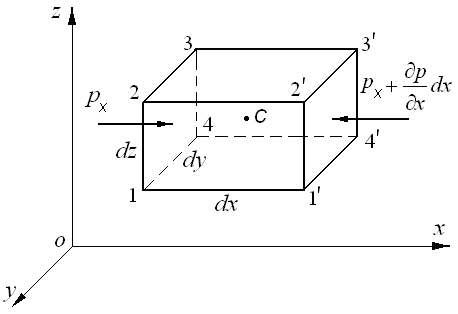
Рис. 2.6. Схема для вывода дифференциальных
уравнений равновесия жидкости
Введём обозначения:
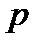- среднее гидростатическое давление на площадку 
;
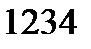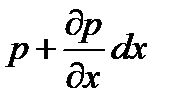- среднее гидростатическое давление на площадку 
;
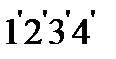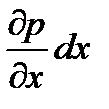- дифференциал, который выражает изменение давления от точки к точке вдоль оси 
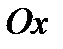при расстоянии между точками 
;
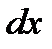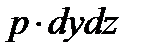- сила гидростатического давления на площадку 
;
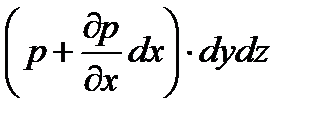- сила гидростатического давления на площадку 
;
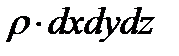- масса параллелепипеда;
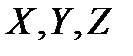- проекции ускорений единичной массовой силы;
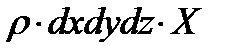- проекция единичной массовой силы на ось 
.
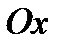На параллелепипед действуют силы гидростатического давления от окружающей жидкости и массовые силы.
Запишем уравнение равновесия в направлении оси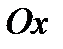 
.
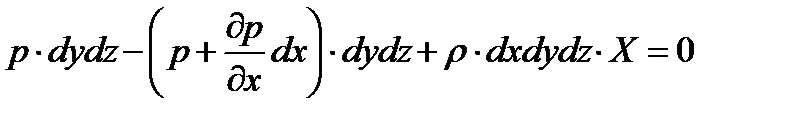После преобразования и деления на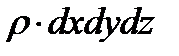 
уравнение примет вид
,
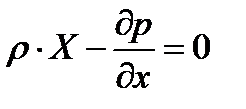или
.
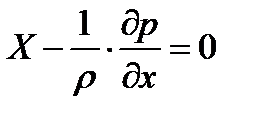Аналогичным образом получим уравнения в направлении осе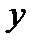й 
и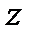 
:
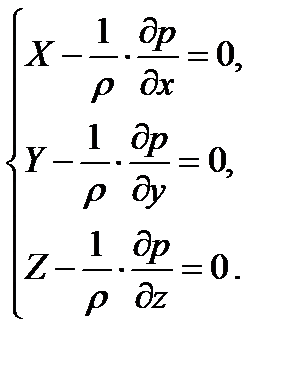(уравнения Эйлера) (2.8)
Полученная система уравнений равновесия жидкости называется уравнениями Эйлер. Они выведены Л.Эйлером в 1755 г.
Слагаемые, входящие в полученные уравнения, являются проекциями единичных массовых и поверхностных сил. Эти уравнения показывают, что поверхностные и массовые силы, действующие на жидкость, взаимно уравновешиваются.
