Найти: 1) математическое ожидание;
2) дисперсию;
3) среднее квадратическое отклонение дискретной случайной величины Х по данному закону ее распределения:
| Вариант № | |
| 1. | xi | | | | | |
| pi | 0,1 | 0,2 | 0,1 | 0,2 | 0,4 |
| 2. | xi | | | | | |
| pi | 0,3 | 0,1 | 0,3 | 0,2 | 0,1 |
| 3. | xi | | | | | |
| | pi | 0,5 | 0,1 | 0,2 | 0,1 | 0,1 |
| 4. | xi | | | | | |
| pi | 0,1 | 0,2 | 0,3 | 0,2 | 0,2 |
| 5. | xi | | | | | |
| pi | 0,2 | 0,2 | 0,4 | 0,1 | 0,1 |
| 6. | xi | | | | | |
| pi | 0,4 | 0,1 | 0,3 | 0,1 | 0,1 |
| 7. | xi | | | | | |
| pi | 0,2 | 0,1 | 0,4 | 0,2 | 0,1 |
| 8. | xi | | | | | |
| pi | 0,1 | 0,2 | 0,4 | 0,2 | 0,1 |
| 9. | xi | | | | | |
| pi | 0,1 | 0,4 | 0,3 | 0,1 | 0,1 |
| 10. | xi | | | | | |
| pi | 0,1 | 0,2 | 0,2 | 0,1 | 0,4 |
Задача №4
Три сотрудника могут составить один и тот же документ. Вероятность представить готовый документ без ошибок для них соответственно равны 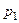 ,
, 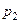 ,
, 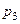 . Составить закон распределения случайной величины
. Составить закон распределения случайной величины 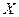 – числа готовых документов без ошибок, найти её математическое ожидание, дисперсию и среднее квадратическое отклонение.
– числа готовых документов без ошибок, найти её математическое ожидание, дисперсию и среднее квадратическое отклонение.
| Вариант № | 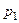 | 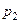 | 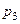 |
| | 0,9 | 0,4 | 0,5 |
| | 0,6 | 0,3 | 0,2 |
| | 0,8 | 0,4 | 0,1 |
| | 0,7 | 0,4 | 0,9 |
| | 0,5 | 0,8 | 0,6 |
| | 0,2 | 0,7 | 0,6 |
| | 0,7 | 0,2 | 0,5 |
| | 0,4 | 0,8 | 0,5 |
| | 0,7 | 0,8 | 0,1 |
| | 0,3 | 0,1 | 0,4 |
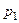 ,
, 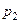 ,
, 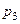 . Составить закон распределения случайной величины
. Составить закон распределения случайной величины 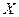 – числа готовых документов без ошибок, найти её математическое ожидание, дисперсию и среднее квадратическое отклонение.
– числа готовых документов без ошибок, найти её математическое ожидание, дисперсию и среднее квадратическое отклонение.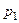
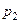
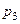
 2015-06-14
2015-06-14 968
968








