| Школы | Число сдавших | Число несдавших | Всего | Долевые отношения | ||
| 1-я | А | В | 53,5% | |||
| (66,9) | (33,0) | (100) | ||||
| 2-я | С | D | 46,5% | |||
| (58,9) | (28,1) | (87) | ||||
| Всего | 100% |
Получены разности по клеткам (знак разности несуществен).
Клетки
A: fA=82-66,9=15,1
В: fB=18-33=15,0
С: fC=44-58,9=14,9
D: fD=43-28,1=14,9
Формула хи-квадрат:
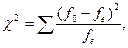
где f0– наблюденные численности, fe– предполагаемые (теоретические) численности.
В рассмотренном материале
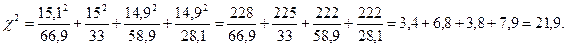
Для получения числа степеней свободы нужно воспользоваться формулой (только для хи-квадрат) fd=(k–1)(с–1)=(2–1)(2–1)=1, т.е. Одна степень свободы, где k – число столбцов, с – число строк с анализируемым материалом.
Обратимся к таблице уровней значимости для одной степени свободы для хи-квадрат (см. Приложение 3, табл. 7): χ20,99=6. Следовательно, полученная величина χ2 вполне достаточна для отклонения Н0. Есть все основания для содержательного вывода о различной подготовленности выпускников 1-й и 2-й школ к экзаменам в вузы. Заметим, что все вычисления, здесь приводимые, ведутся с точностью до первого или второго знака, т.е. вычисляются целью и десятые, редко – сотые. Этим объясняется, в общем-то, несущественная разница при вычислениях одной и той же величины разными способами. Никакого практического значения встречающиеся расхождения в величинах не имеют.
Полезно знать, что коэффициент хи-квадрат и коэффициент четырехпольной корреляции взаимосвязаны, и поскольку известны численность и распределение сопоставляемых выборок, указанные коэффициенты могут быть определены один через другой.
Как показывает само название этого метода, числовой материал, подлежащий статистическому анализу, может быть распределен в таблице графике, имеющей четыре поля (табл. 15). Такое расположение мат риала облегчает все последующие действия с ним. Чтобы рассмотреть технику вычисления коэффициента четырехпольной корреляции он обозначается символом φ (фи), – можно воспользоваться примером, в котором речь шла о вычислении коэффициента χ2.
Выпускники двух школ сравнивались междусобой по подготовленности к вузовским экзаменам.
Таблица 15
 2015-06-14
2015-06-14 715
715








