Информационные характеристики средств измерений

С точки зрения теории информации суть измерения состоит в сужении интервала неопределенности меры информации от значения, известного перед его проведением, до величины, называемой энтропийным интервалом неопределенности 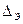. Чтобы оценить этот интервал, рассмотрим некоторые элементы теории информации.

Одним из основных понятий теории информации является так называемая безусловная энтропия 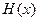, которая для плотности вероятности распределения погрешностей 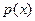определяется как .

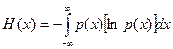Безусловная энтропия характеризует неопределенность наших знаний (сведений), остающуюся после получения (измерения) значения измеряемой величины при свойственной ей законе распределения вероятностей.

Согласно основному положению теории информации (теорема Шеннона): Количество информации I, получаемое в результате измерения, равно уменьшению неопределенности, т.е. разности энтропий до и после измерения:

.

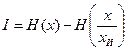Здесь 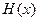- безусловная (априорная) энтропия; 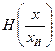- условная (апостериорная) энтропия, т.е энтропия величины х при условии, что получен результат .

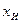Очевидно, что условная энтропия определяется законом распределения погрешности ∆ СИ:

.

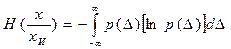Если погрешность измерения распределена равномерно на некотором интервале (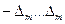), то условная энтропия .

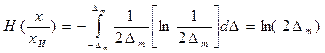Для нормального закона распределения с СКО σ условная энтропия

.

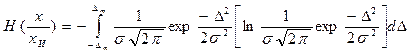Опустив выкладки, запишем: 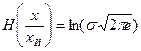, где 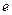- основание натурального логарифма.

Из сравнения формул равномерного и нормального законов распределения можно заметить, что измерительные приборы, имеющие различные законы распределения погрешностей, при измерении одной и той же величины могут давать одинаковое количество информации. В нашем случае это 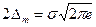. Поэтому в качестве характеристики дезинформационного воздействия на точность измерения погрешности с произвольным законом распределения, используют ее энтропийное значение.

В метрологии под энтропийным значением погрешности измерения принято считать наибольшее значение погрешности при равномерном законе распределения, которая вносит такое же дезинформационное действие, как и погрешность с любым другим законом распределения.

Так, например, если погрешность измерения распределена нормально, то энтропийное значение погрешности 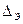= 0,5 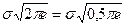≈ 2,07 σ.

В общем виде зависимости между энтропийным значением и значением СКО погрешности представляют как 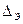= 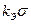, где 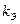- энтропийный коэффициент. Энтропийный коэффициент 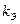зависит от вида закона распределения погрешностей. Для равномерного распределения энтропийный коэффициент равен 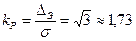. Для нормального распределения .

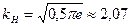При одинаковых средних квадратических значениях погрешности дезинформационное действие погрешности с любым законом распределения меньше дезинформационного действия погрешности, распределенной по нормальному закону.

Для доказательства этого положения сравним два прибора, предназначенных для измерения одной и той же физической величины, но имеющих разные законы распределения погрешности.

Пусть абсолютная погрешность первого прибора имеет равномерное распределение на интервале (-10^-2, 10^-2), а погрешность второго прибора – нормальное с нулевым математическим ожиданием и СКО 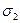= 0,5·10^-2.

Сравним эти приборы по точности, выбрав в качестве критерия следующие параметры: наибольшую погрешность, СКО погрешности и энтропийную погрешность.

Первый прибор имеет наибольшее значение абсолютной погрешности измерений ∆ = 10^-2.

Погрешность второго прибора не ограничена, ее наибольшее значение в принципе равно бесконечности. На практике для нормального закона часто используют значение «трех сигм», принимая максимальную абсолютную погрешности 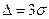. В данном случае ∆=1,5·10^-2. по этому критерию следует отдать предпочтение первому прибору, однако нельзя считать достаточно обоснованным принятое значение наибольшей погрешности второго прибора. СКО погрешности первого прибора 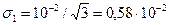, следовательно, по этому критерию следует отдать предпочтение второму прибору, у него 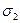= 0,5·10^-2.

При информационном подходе к измерениям используют сравнение приборов по количеству информации, получаемой при измерении, т.е. по энтропийному значению погрешности.

Для первого прибора мы имеем 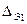= =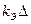1,73·10^-2.

Для второго прибора 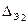= =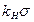2,07·0,5·10^-2 = 1,035·10^-2.

Анализ полученных энтропийных значений погрешностей показывает, что по информационному критерию эти приборы отличаются существенно.