Основные понятия теории случайных погрешностей

Случайная погрешность при измерении одной и той же постоянной во времени физической величины (параметра) возникает при одновременном влиянии на показания прибора многих взаимонезависимых источников (нестабильность питающей сети, электромагнитные наводки, флуктуации в компонентах и т.п.), которые в каждый данный момент проявляются по−разному.

При проведении повторных наблюдений за показаниями измерительного прибора в неизменных условиях каждая из множества причин случайных изменений показаний может или проявиться или не проявиться. В итоге, случайные изменения показаний, появляющиеся при каждом наблюдении, могут быть любыми как по размеру, так и по знаку. Таким образом, при многократных наблюдениях, результат наблюдений Q может быть, в некоторых случаях, незначительно подвержен влиянию случайной погрешности, так как различные по знаку случайные погрешности могут частично компенсировать друг друга.

Влияние случайной погрешности на результат измерений Q можно оценить при помощи приемов математической статистики (теоретической основой которой является теория вероятностей, изучающая поведение и описание случайных величин). Основные способы описания случайных погрешностей с помощью теории вероятностей и математической статистики заключаются в следующем.

Если весь диапазон Q _min.... Q _max результатов n наблюдений величины Q разбить на несколько одинаковых интервалов шириной d Q и подсчитать, сколько результатов наблюдений попало в каждый интервал (m_i), то всю совокупность результатов наблюдений можно представить в виде ступенчатой кривой − гистограммы W(Q). Такая кривая W(Q) отражает характер распределения (группирования) случайной погрешности и результатов наблюдений в диапазоне Q _min.... Q _max (рис.5.1).

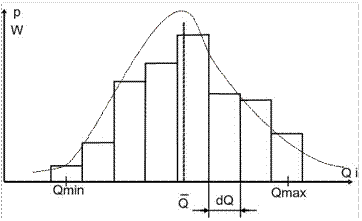
Рисунок5.1 – Гистограмма(W) и полигон(r) распределения

Если наблюдения продолжать очень долго, т.е. n®¥, а при построении гистограммы количество интервалов увеличивать, т.е. d Q ®0, то вместо гистограммы может получиться плавная кривая r (Q), которая называется полигоном распределения и характеризирует собой плотность распределения вероятностей. Смысл этой плавной кривой состоит в том, что произведение r (Q)*d Q дает долю полного числа отсчетов n, приходящихся на интервал от Q до Q +d Q. Иначе говоря, произведение r (Q)*d Q есть вероятность того, что отдельное наблюдение Q i окажется в интервале Q +d Q.

Наиболее общие стандартные функции распределения случайных погрешностей представлены в табл.5.1.

Таблица 5.1 − Стандартные аппроксимации функций распределения

Распределе-ние	Плотность вероятности	Ki
Аналитическое представление	Графическое представление	Dпр/σQ
Нормаль− ное (норм.)		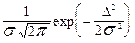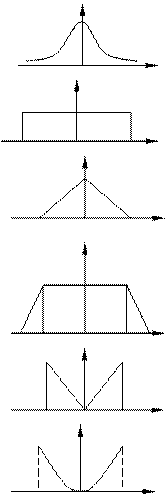f(D) D	3,0
Равномер ное (равн.)		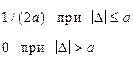f(D) D −a a	√3≈ 1,7
Треуголь ное (Симпсона)		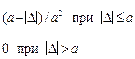f(D) D −a a	2,4
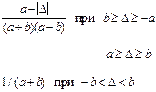Трапецевидное (трап.)		f(D) −a −b b a D	2,3
Анти модальное (ам)		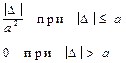f(D) D −a a	1,4
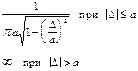Арксинуса		f(D) D −a a	1,4

Из всех распределений, представленных в табл.5.1, наиболее часто при анализе и оценке случайных погрешностей встречается нормальное распределение, аналитическое выражение которого имеет вид

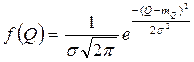(5.4)

где f (Q) − плотность вероятности;

− s − дисперсия результатов наблюдений;

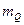− − математическое ожидание результатов наблюдений.

Математическое ожидание 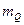− это значение случайной величины, соответствующее наибольшей вероятности его появления, вокруг которого группируются результаты отдельных наблюдений Q_і. Если систематическая погрешность при измерениях исключена (D_сист = 0), и результаты наблюдений распределены по нормальному закону, то математическое ожидание будет соответствовать истинному значению измеряемой величины.

Среднеквадратическое отклонение б_Q, или дисперсия б²_Q, является числовой характеристикой степени рассеивания результатов наблюдений относительно математического ожидания.

На рис.5.2 изображены графики нормального распределения результатов наблюдений при б_Q' > б_Q'' > б_Q''' и одном и том же математическом ожидании.

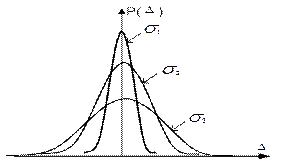
Рисунок 5.2− Графики нормального распределения результатов наблюдений

Сравнение графиков показывает, что с увеличением б_Q рассеивание результатов относительно m_Q увеличивается, т.е. вероятность больших погрешностей увеличивается, а малых погрешностей уменьшается.

Зная закон распределения случайной погрешности, можно ответить на вопрос: какая доля результатов измерений попадает в интервал Q _min... Q _max?

Эту долю всех результатов наблюдений, называют доверительной вероятностью Р, а интервал, в который попадает значение случайной величины с заданной доверительной вероятностью, называется доверительным интервалом. Очевидно, что, значение Р(Q) − это площадь под кривой r(Q) в диапазоне значений Q _min... Q _max. При Q _min = −¥ и Q _max = +¥ Р(Q) =1 (100 %), поскольку появление показания измерительного прибора в таком диапазоне значений является достоверным событием. Так, при нормальном законе распределения случайной погрешности вероятность попадания результата наблюдений в интервал (m_Q ± б_Q) оказывается равной 68,26 %, для интервала (m_Q ± 2б_Q) − 95,44% для интервала (m_Q ± 3б_Q) − 99,73 %.

Погрешность, равную ± 3б_Q, которой соответствует доверительная вероятность 99,73%, называют предельной погрешностью D_пр. Для стандартных аппроксимаций функций распределения погрешности значения D_пр/б_Q приведены в табл.5.1.