2015-06-16
2958
В процессе конвективного переноса теплоты характер течения жидкости имеет очень большое значение, так как им определяется механизм теплоотдачи. Процесс переноса теплоты на границе с поверхностью канала может быть выражен законом Фурье
|
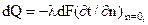
где n— нормаль к поверхности тела.
Это же количество теплоты можно выразить уравнением Ньютона – Рихмана
|
.
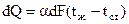Приравнивая эти уравнения, получим
|
,
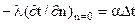или
|
.
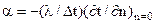Дифференциальное уравнение (4.12) описывает процесс теплообмена на поверхности канала (n = 0).
Уравнение (4.4) показывает, что коэффициент теплоотдачи — величина сложная и для ее определения невозможно дать общую формулу. Обычно для определения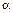 
приходится прибегать к опытным исследованиям.
Применяя общие законы физики, можно составить дифференциальные уравнения для конвективного теплообмена, учитывающие как тепловые, так и динамические явления в любом процессе.
Система дифференциальных уравнений состоит из уравнений энергии (или теплопроводности), теплообмена, движения и сплошности.
Дифференциальное уравнение энергии устанавливает связь между пространственным и временным изменением температуры в любой точке движущейся жидкости:
|
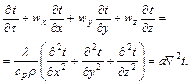
Если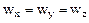 
= 0, уравнение энергии переходит в уравнение теплопроводности для твердых тел (если отсутствуют внутренние источники теплоты).
Дифференциальное уравнение теплообмена выражает условия теплообмена на границе твердого тела и жидкости:
|
.
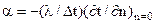Дифференциальное уравнение движения вязкой несжимаемой жидкости представлено уравнением Навье-Стокса:
для оси x
|
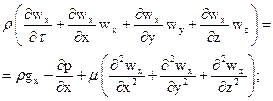
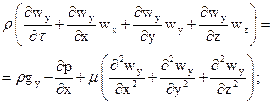
для оси z
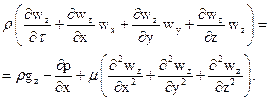
Это уравнение справедливо для ламинарного и турбулентного движений. В последнем случае w представляет собой действительную (мгновенную) скорость, равную сумме средней и пульсационной скоростей.
Дифференциальное уравнение сплошности, или непрерывности, для сжимаемых жидкостей имеет вид
|
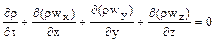. Для несжимаемых жидкостей при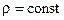 
уравнение сплошности принимает вид
|
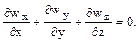
Вывод всех дифференциальных уравнений (4.13) — (4.17) требует громоздких математических выкладок и приводится в специальных курсах гидродинамики и теплопередачи.
4.3. Краевые условия.
Система дифференциальных уравнений для процессов конвективного теплообмена охватывает бесчисленное множество процессов теплоотдачи, которые описываются этими уравнениями, но вместе с тем каждый из них отличается от других некоторыми частностями. Чтобы ограничить задачу и из бесчисленного множества выделить рассматриваемый процесс и определить его однозначно, т.е. дать полное математическое описание, к системе дифференциальных уравнений необходимо присоединить еще математическое описание всех частных особенностей, которые называются условиями однозначности или краевыми условиями.
Условия однозначности состоят из:
геометрических условий, характеризующих форму и размеры системы, в которой протекает процесс;
физических условий, характеризующих физические свойства среды и тела;
граничных условий, характеризующих особенности протекания процесса на границах тела;
временных условий, характеризующих особенности протекания процесса во времени.
Когда условия однозначности для какого-либо конкретного случая заданы, то они вместе с системой дифференциальных уравнений составляют математическое описание данного процесса. Тем самым после решения системы уравнений можно получить полное описание процесса во всех деталях: поля температур, скоростей, давлений и т. д.
Условия однозначности могут быть заданы в виде числовых значений, в виде функциональных зависимостей или в табличной форме. Пусть, например, рассматривается случай теплоотдачи при движении жидкости в трубе. В этом случае могут быть заданы такие условия однозначности:
1. Труба круглая, гладкая, внутренний диаметр трубы d и длина l.
2. Рабочим телом, т. е. теплоносителем, является вода, которая несжимаема, ее физические свойства равны: λ (t), c (t), μ (t) и ρ (t). Если же зависимостью физических свойств от температуры можно пренебречь, тогда они задаются просто в виде числовых значений λ, с, μ, и ρ.
3. Температура жидкости на входе равна t'ж, а на поверхности
трубы tc. Скорость на входе равна w, а у самой стенки w = 0. Если же температура и скорость на входе не постоянны, то должен быть
задан закон их распределения по сечению.
4. Для стационарных процессов временные условия однозначности отпадают.
Итак, математическое описание процесса теплоотдачи состоит из: 1) уравнения теплопроводности; 2) уравнения движения; 3) уравнения сплошности; 4) уравнения теплообмена и условий однозначности.
К настоящему времени аналитические решения системы дифференциальных уравнений конвективного теплообмена получены лишь для ограниченного числа простейших задач при введении тех или иных упрощающих допущений. Такое положение объясняется большой сложностью уравнений или в конечном счете сложностью и многогранностью содержания самих процессов.
Вследствие ограниченности возможностей аналитического решения приведенных выше дифференциальных уравнений большое значение в изучении процессов теплоотдачи приобретает эксперимент. Экспериментальное изучение сложных процессов, зависящих от большого числа отдельных факторов, само по себе является трудным делом. Кроме того, при постановке эксперимента, помимо подробного изучения рассматриваемого процесса, обычно всегда ставится также задача получить данные для расчета других процессов, родственных изучаемому.
Следовательно, если недостатком экспериментального метода исследования является невозможность распространения результатов, полученных в данном опыте, на другие явления, отличающиеся от изученного, то недостатком математической физики является невозможность перейти от класса явлений, характеризуемых дифференциальными уравнениями и условиями однозначности, к единичному конкретному явлению. Каждый из этих методов в отдельности не может быть эффективно использован для решения практических задач.
Если положительные стороны математического и экспериментального методов исследования объединить в одно целое, то можно получить универсальный аппарат для изучения различных явлений природы. Такое объединение обоих методов осуществляется теорией подобия.
