Решение

Введем обозначения:

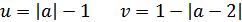
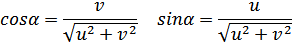
Тогда:

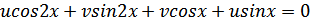
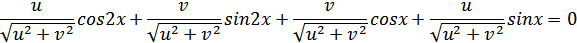
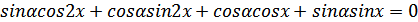
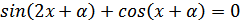
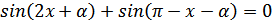
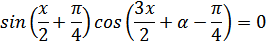
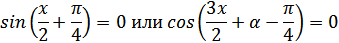
1.

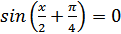
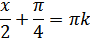
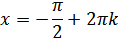
2.

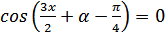
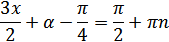
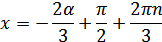
Нам надо, чтобы было нечетное число корней. Первое уравнение одно решение 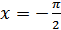. Второе давать 3 решения на периоде (это становится понятным, если посмотреть на слагаемое )

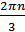Таким образом, нечетное число корней (а точнее – 3 корня) будет если одно из решений второго уравнения совпадает с 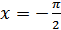или попадает в точку π, т.е. не входит в рассматриваемый промежуток.

Рассмотрим эти случаи.

1.

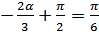
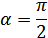
Тогда: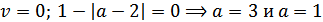

Но при а=1 u=0, а это невозможно.

2.

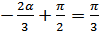
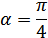
Тогда: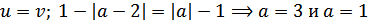

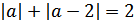
а)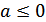

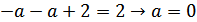
б)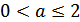

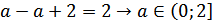
в)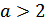

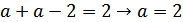
Т.о.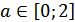

Ответ: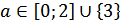

С5 Найти все значения параметра а, при которых система 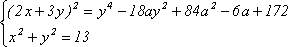имеет хотя бы одно решение. Найдите эти решения.