В каждой точке, в которой она определена

Свойства н епрерывных на отрезке функции: 1) Вейерштрасса- Если функция непрерывна на отрезке,

то она достигает на этом отрезке своего наибольшего и наименьшего значений.2) Если функция непрерывна на отрезке, то она ограничена на этом отрезке.3) (Больцано-Коши)- Если функция у = f(x) непрерывна на отрезке [а; b] и принимает на его концах неравные значения f(а) = А и f(b) = В, то на этом отрезке она принимает и все промежуточные значения между А и В.

Точки, в которых нарушается непрерывность функции, наз точками разрыва этой функции. Если x = 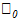— точка разрыва функции у = f(x), то в ней не выполняется по крайней мере одно из условий первого определения непрерывности функции;1- Функция определена в окрестности точки хо, но не определена в самой точке хо.2- Функция определена в точке хо и ее окрестности, но не сущ-ет предела f(x) при ng w:fareast="RU"/></w:rPr><m:t>x</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Times New Roman" w:fareast="Times New Roman" w:h-ansi="Times New Roman"/><wx:font wx:val="Times New Roman"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/><w:lang w:fareast="RU"/></w:rPr><m:t>0</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 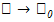. 3-Функция определена в точке 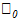и ее окрестности, сущ-ет 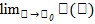,но этот предел не равен значению функции в точке Хо. ()

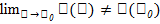Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Точка разрыва 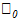называется точкой разрыва 1-го рода f у = f(x), если в этой точке сущ-ют конечные

пределы f слева и справа (односторонние пределы), т. е 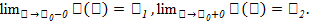При этом: а) если A1 = А2, то точка 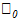наз точкой устранимого разрыва; б) если А1 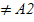, то точка 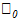наз точкой конечного разрыва. Величину 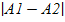наз скачком функции в точке разрыва первого рода. Точка разрыва 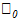наз точкой разрыва второго рода функции у = f(x), если по крайней мере один из односторонних пределов (слева или справа) не существует или равен бесконечности.

ВОПРОС 5 Дифференцируемость функции, производная, дифференциал.

Задачи, приводящие к понятию производной

Задача о скорости. Пусть материальная точка М движется неравномерно по нек. прямой. Каждому значению времени t соответствует определенное расстояние ОМ = S до некоторой фиксированной

точки О. Это расстояние зависит от истекшего времени t, т. е. S = S(t). Это равенство наз законом движения точки. необходимо найти 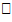движения точки. Если в некоторый момент времени t

точка занимает положение М, то в момент времени t + > 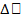точка займет положение М1, где ОМ1 =

= S + S. т.о., перемещениеточки М за время t будет S =S(t + t) - S(t). 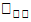за промежуток времени 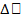определяется отношением 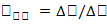пройденного пути ко времени. Предел 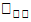движения при t 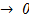наз скоростью движения точки в данный момент времен и (Обозначив эту скорость через V, получим: .

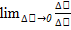К нахождению пределов приводят решения и множества других задач. Можно показать, что:-

Пределы имеют одинаковый вид; везде требуется найти предел отношения приращения функции к приращению аргумента. Этот предел называют производной.

Задача о плотности стержня. Пусть дан тонкий прямолинейный неоднородный стержень длиной l. Определим плотность стержня в любой его точке. Пусть стержень расположен на оси Ox, причем один из его концов совпадает с началом координат. Тогда каждой точке стержня соответствует определенная координата x. Обозначим через m массу отрезка стержня между точками с координатами 0 и х. Ясно, что m явл f 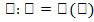. Рассмотрим две точки стержня: фиксированную точку 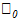и переменную точку 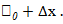Отрезок стержня, расположенный между этими точками, имеет длину 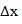и массу 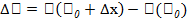. Отношение 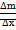наз средней плотностью стержня на отрезке от точки 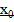до точки 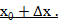Плотностью стержня в точке 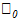наз предел средней плотности, когда длина отрезка 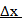стремится к нулю: Данные задачи, несмотря на их различное физ. содержание, привели к нахождению предела одного и того же вида — пределу отношения приращения функции к приращению аргумента. т.е. Производной 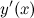от функции 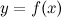в точке 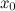назпредел отношения приращения функции 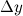к приращению аргумента 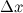когда приращение аргумента 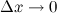. Приращением аргумента назразность между двумя значениями аргумента: "новым" и "старым" 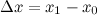. Приращением функции 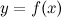в точке 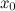, соответствующее приращению аргумента 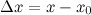, наз величина: 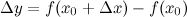. Производная функции f(x) есть некоторая f 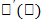, произведенная из данной f. Геометрический смысл производной: 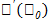явл угловым коэффициентом касательной к графику функции y=f(x)в точке с абсциссой 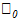имеет вид 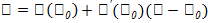Угловой K прямой равен tg угла, образованного этой прямой с "+" направлением оси Ох. Механический смысл производной: Пусть S=S(t) – уравнение зависимости пути от времени при движении тела. Тогда 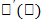– скорость движения этого тела в момент времени t. 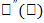-ускорение движущегося тела в момент времени t.

Функция у = f(x) имеющая производную в каждой точке интервала (а;b), наз дифференцируемой в этом интервале и операция нахождения производной функции наз дифференцированием этой функции. Функция 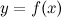имеет производную на интервале 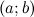или наз дифференцируемой в этом интервале, если производная 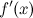сущ-ет в каждой точке этого интервала.

Функция 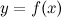имеет в точке бесконечную производную, если в этой точке 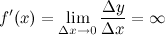. Теорема (О необходимом и достаточном условии дифференцируемости)

Для того чтобы функция 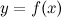была дифференцируемой в точке , необходимо и достаточно, чтобы 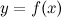имела в этой точке конечную производную. Дифференциалом функции называется линейная относительно 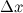часть приращения функции. Она обозначается как 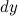или 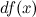. Таким образом: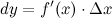

Замечание Дифференциал функции составляет основную часть ее приращения.

Замечание Наряду с понятием дифференциала функции вводится понятие дифференциала аргумента. По определению дифференциал аргумента есть приращение аргумента: 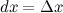Замечание Формулу для дифференциала функции можно записать в виде: 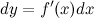. Отсюда получаем, что 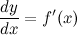Итак, это означает, что производная может быть представлена как обыкновенная дробь - отношение дифференциалов функции и аргумента. Геом. смысл дифференциала -Дифференциал функции в точке 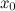равен приращению ординаты касательной, проведенной к графику функции в этой точке, соответствующему приращению аргумента .

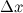Правила дифференцирования: 1. Если функции 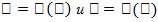дифференцируемы в данной точке х, то в той же точке дифференцируема и их сумма, причем производная суммы равна сумме производных слагаемых: 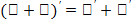.2. Если функции 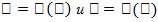дифференцируемы в данной точке х, то в той же точке дифференцируемо и их произведение. При этом производная произведения находится по след. фор.: 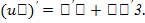. Если есть две функции f (x) и g (x), причем g (x) ≠ 0 на интересующем нас множестве, можно определить новую функцию h (x) = f (x)/ g (x). Для такой функции тоже можно найти производную: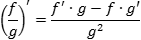

Пусть у = f(u) и y= 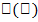тогда y= 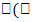— сложная функция с промежуточным аргументом и и независимым аргументом х. Теорема:. Если функция y= 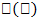имеет производную и'х в точке

х, а функция у = f(u) имеет производную у'и в соответствующей точке u = 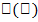, то сложная функция у = y= 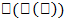имеет производную у'х в точке х, которая находится по формуле у'х = у'и и'х.

Д/ нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по

независимому аргументу. Это правило остается в силе, если промежуточных аргументов несколько. Так, если у = f(u), u = 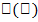, v = g(x), то 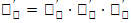. Пусть у = f(x) и х = 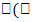) — взаимно обратные функции. Теорема: Если функция у = f(x) строго монотонна на интервале(a; b) и имеет неравную нулю производную f'(x) в произвольнойточке этого интервала, то обратная ей функция х = 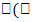) также имеет

производную 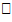'(у) в соответствующей точке, определяемую равенством 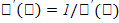или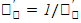

Т.О производная обратной функции равнаобратной величине производной данной функции. Правило дифференцирования обратной функции: 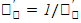. Производные основных элементарных функций: 1) степенная( 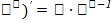2)показательная 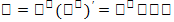. 3) логарифмическая 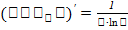. 4) тригонометрическая- 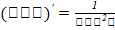и обратные тригонометрические

Основными теоремами дифференциального исчисленияявл лемма Ферма и теорема РолляТ: Ролля- Если ff(x) непрерывна на отрезке [а;в], дифференцируема на интервале (a;b) ии на концах отрезка принимает один.значенияf(a)=f(b), то найдется хотя бы одна точка с принадлеж. (а;в), в к. производная обращается в ноль.Если функция задана уравнением у = f(x), разрешенным относительно у, то функция задана в явном виде (явная функция).Под неявным заданием функции понимают задание функции ввиде уравнения F(x; у) = 0, не разрешенного относительно у. Если неявная функция задана уравнением F(x; у) = 0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по х, рассматривая, при этом у как функцию х, и полученное затем уравнение разрешить относительно у'. Производная неявной функции выражается через аргумент х и

функцию у. Так как функция /(ж) непрерывна на отрезке [а; 6], то она достигает на этом отрезке своего наибольшего и наименьшего значений соответственно, М и m. Если М = т, то функция /(ж)

постоянна на [a; b] и, след, ее производная f'(x) = 0 в любой точке отрезка [а, в].Геометрически теорема Ролля означает, что на графике функции у = f(x) найдется точка, в которой касательная к графику параллельна оси Ох Т.Коши- Если функции f(х) и фи(x) непрерывны на отрезке [a;b], дифференцируемы на интервале (а; b), причем 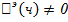для х € (а; b), то найдется хотя бы одна точка на интервале 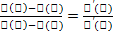. Т. Лагранджа-если функция непрерывна на отрезке и дифференцируема на интервале, то найдется х.б. 1 точка с, такая, что выполняется условие-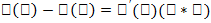

Вопрос 6 Неопределенный интеграл и основные методы интегрирования.

В дифференциальном исчислении решается задача: по данной функции f (х) найти ее производную (или дифференциал). Интегральное исчисление решает обратную задачу: найти функцию F(x), зная

ее производную F'(x) = f(x) (или дифференциал). Искомую функцию F(x) называют первообразной функции f(x). Функция F(x) наз первообразной функцией f(x) на нек. промежутке х, если для всех значений х этого промежутка выполняется след. условие: 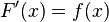.Н: первообразной fy=x^2=F(x)=x^3/3. Т-ма. Если функция F(x) является первообразной функции f(x) на (а; Ь), то множество всех первообразных для f(x) задается формулой F(x) + С, где С — постоянное число. Неопределённый интегра́л от функции F(x)+C для f(x) — это множество всехпервообразных данной функции.Если функция 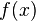определена и непрерывна на промежутке 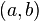и 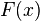— её первообразная, т.е. 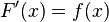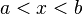при , то

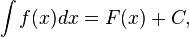
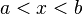, С-const.

Геометрически неопределенный интеграл представляет собой семейство ≪параллельных≫ кривых у = F(x) + С (каждому числовому значению С соответствует определенная кривая семейства) График каждой первообразной (кривой) называется интегральной кривой.

Свойства неопределенного интеграла: 1. Производная неопределенного интеграла равна подинтегральной функции:

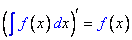
2. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной: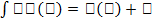

3/ Постоянный множитель можно выносить за знак интеграла: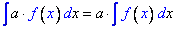

3. Неопределенный интеграл от дифференциала некоторой функции равен сумме самой этой функции и произвольной постоянной: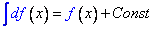

4. Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от слагаемых функций: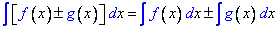

5. Свойство инвариантности неопределенного интеграла:

Если 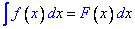, то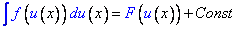

Основные методы интегрирования:1. метод непосредственного интегрирования - метод вычисления интегралов с помощью таблицы простейших интегралов и основных свойств неопределенных интегралов. 2. метод подстановки(м. замены переменных)- Метод нтегрирования подстановкой заключается во введении новой переменной интегрирования (т. е. подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся (в случае ≪удачной≫ подстановки). Общих методов подбора подстановок не существует. / интегралы сводятся к табличным и далее выполняется интегрирование.3. - Пусть и = и(х) и v = v(x) — функции, имеющие непрерывные производные. Тогда d(uv) = и ■ dv + v ■ du. Интегрируя это равенство,

получим метод по частям-основан на использовании формулы: 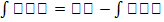. формулой интегрирования по частям. Она дает возможность свести вычисление интеграла

J и dv к вычислению интеграла j vdu, который может оказаться существенно более простым, чем исходный. Интегрирование по частям состоит в том, что подынтегральное выражение заданного интеграла представляется каким-либо образом в виде произведения двух сомножителей и и dv (это, как правило, можно осуществить несколькими способами); затем, после нахождения v и du, используется формула интегрирования по частям. Иногда эту формулу приходится использовать несколько раз.

Вопрос 7: Определенный интеграл.

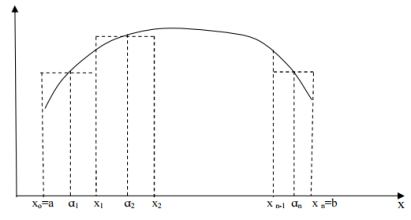
Пусть на отрезке [ab] дана непрерывная функция y=f(x). Необходимо найти площадь криволинейной трапеции (криволинейная трапеция- часть плоскости, заключенная между графиком функции, осью ОХ и вертикальными прямыми х=а и х=b)

1. Разобьем отрезок [ab] на n отрезков точками xo=a, x1, x2 …….. x n=b. Длина каждого из отрезков будет равна: ∆x= 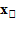- x1,…., ∆ 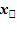= 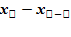. Внутри каждого отрезка разбиения возьмем точки 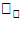, 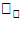…. 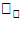и вычислим значения функции в этих точках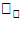: f(), f(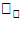),….., f(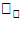). Составим сумму площадей полученных прямоугольников: 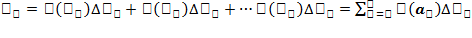. Данная сумма наз интегральной суммой функции y=f(x) на отрезке [a,b] и представляет собой сумму площадей всех прямоугольников и, след, приближенно выражает площадь криволинейной трапеции, и тем точнее, чем больше число участков разбиения и чем меньше длина каждого из них. Определенным интегралом от функции y=f(x) на отрезке [a,b] называется предел интегральной суммы (1), когда число участков разбиения стремится к бесконечности, а длина каждого из них стремится к нулю: 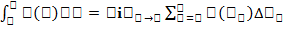. Где a и b называются пределами интегрирования, причем а – нижний предел интегрирования, а b – верхний предел интегрирования. Геометрический смысл определенного интеграла- Если функция y=f(x) непрерывна и положительна на некотором отрезке [a;b], то интеграл 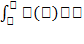равен площади криволинейной трапеции, к. ограничена осью абсцисс, графиком функции y=f(x) и вертикальными прямыми x=a и x=b. 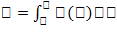. Физ. смысл определенного интеграла - п усть некоторая материальная точка M перемещается под действием силы F=F(x), к. направлена вдоль оси абсцисс (здесь x – абсцисса движущейся точки M).Работа переменной силы F, величина к. есть непрерывная функция F=F(x), действующей на отрезке [a;b], равна определенному интегралу от величины F(x) силы, взятому по этому отрезку: 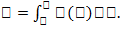Св-ваопред. инт: 1. const выносится за знак интеграла. 2. определ. интеграл меняет знак при перестановке пределов интегрирования. 3. Если пределы интегрирования одинаковы, то интеграл =0. 4.Определенный интеграл от суммы функций равен сумме интегралов от этих функций. 5. Определенный интеграл от единицы равен длине интервала интегрирования. 6.Определенный интеграл от неположительной функции всегда меньше или равен нулю. (Теорема существования определенного интеграла). Если функция y=f(x) непрерывна на отрезке [a,b], то интеграл от этой функции на данном отрезке существует. Теорема 2. Если функция f(x) непрерывна на интервале [a;b] и F(x) явл ее первообразной, то определенный интеграл от функции f(x) на [a;b] = разности значений первообразной по верхнему и нижнему пределам интегрирования, т.е. 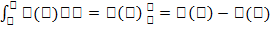наз формулой Ньютона-Лейбница.

Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий.

· Область интегрирования является бесконечной. Например, является бесконечным интервалом .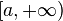

· Функция 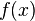является неограниченной в окрестности некоторых точек области интегрирования.

Если интервал 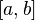конечный, и функция интегрируема по Риману, то значение несобственного интеграла совпадает с значением определённого интеграла.

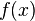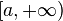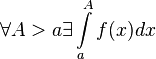Несобственные интегралы I рода-Пусть определена и непрерывна на множестве от и . Тогда:

1. Если 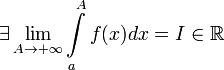, то используется обозначение 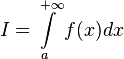и интеграл называется несобственным интегралом Римана первого рода. В этом случае 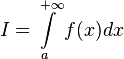называется сходящимся.

2. Если не существует конечного 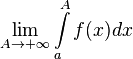( 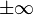или 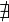), то интеграл 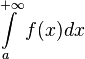называется расходящимся к 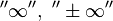, или просто расходящимся.

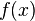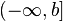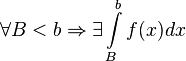Пусть определена и непрерывна на множестве от и . Тогда:

1. Если 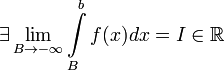, то используется обозначение 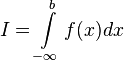и интеграл называется несобственным интегралом Римана первого рода. В этом случае 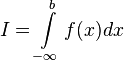называется сходящимся.

2. Если не существует конечного 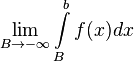( 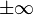или 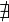), то интеграл 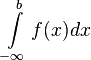называется расходящимся к 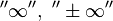, или просто расходящимся.

Если функция 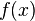определена и непрерывна на всей числовой прямой, то может существовать несобственный интеграл данной функции с двумя бесконечными пределами интегрирования, определяющийся формулой:

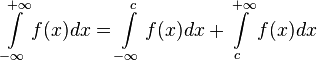, где с — произвольное число.