Геометрический смысл несобственных интегралов II родавыражает площадь бесконечно высокой криволинейной трапеции

вопрос 8 Геометрические приложения определенного интег­рала.

Пусть требуется найти значение какой-либо геом. или физ. величины А (площадь фигуры, объем тела, давление жидкости на вертикальную пластину и т. д.), связанной с отрезком [а;b] изменения независимой переменной х. Предполагается, что эта величина А аддитивна, т. е. такая, что при разбиении отрезка [а; b] точкой с 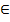(а; b) на части [а; с] и [с; b] значение величины А, оответствующее всему отрезку [а;Ь], равно сумме ее значений, соответствующих [а; с]. Д/нахождения этой величины А можно руководствоваться одной из двух схем: I схема (или метод интегральных сумм) и II схема (или метод дифференциала). I схема базируется на определении определенного интеграла.1. Точками 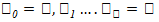разбить отрезок [а;b] на п частей. В соответствии с этим, интересующая нас величина А разобьется на п ≪элементарныхслагаемых≫ А, (i = 1,...,n): А = A1+ 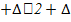An. 2. Представить каждое ≪элементарноеслагаемое≫ в видепроизведения нек.f (определяемойизусловиязадачи), вычисленнойв произвольнойточкесоответствующегоотрезканаегодлину: 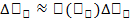. Принахожденииприближенногозначения 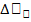, допустимынек. упрощения: дугунамаломучасткеможнозаменитьхордой, стягивающейееконцы; переменнуюскоростьнамаломучасткеможноприближенносчитатьпостоянной и т. д.Получимприближенноезначениевеличины А в видеинтегральнойсуммы и искомая величина A = пределу интегральной суммы: 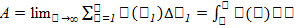– этот метод основан на представлении интеграла как о сумме бесконечно большого числа бм слагаемых., а т.ж. представлена для выяснения геом. И физ. Смысла определенного интгерала. II метод наз≪методдифференциала≫или≪методотбрасывания

бесконечномалыхвысшихпорядков≫: 1) наотрезке [a; b] выбираем произвольное значение х и рассматриваем переменный отрезок [a; х]. На этом отрезке величина А становится f х: А = А (x), т. е. считаем, что часть искомой величины А есть неизвестная функция А(x), где х 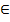[а; b] — одинизпараметроввеличины А; 2) находим главную часть приращения А при изменении х на малую величину x= dx, т. е. находим дифференциал dA функции А = А(х): dA = f{x)dx, где f(x) определяемая из условия задачи, f переменной x; 3) считая, что dA 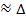А при 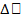—>0, находимискомуювеличинупутеминтегрирования dA в пределах от a до b: 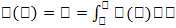Понятие опр. интеграла находит свое применение на практике. В частности, при помощи опр. интегралов можно вычислять площади фигур, длины кривых, объемы тел вращения и т.д. В связи с этим, можно отметить, что определенный интеграл можно использовать только в тех случаях, когда вычисляемую величину можно представить в виде суммы ее частей. След., для таких величин можно составить интегральные суммы при помощи предельного перехода переходить к определенным интегралам.Итак, 1. вычисление площадей плоских фигур - Пусть даны две непрерывные на [a, b] функции f1(x) 6 f2(x), и нам надо найти площадь между ними в пределах отрезка [a, b]. Как это сделать, говорит следующая лемма. Лемма 1.1. Усл.- Функции f1(x) 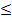f2(x) заданы и непрерывны на [a, b]. Утв. Площадь фигуры, ограниченной графиками f1(x) и f2(x), а также прямыми x = a и x = b, вычисляется по формуле: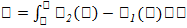

Док-во: Обозначим искомую площадь между графиками через S, площадь под графиком функции f1(x) через S1, а площадь под графиком функции f2(x) через S2. Очевидно, что S1 = S + S2. C другой стороны, 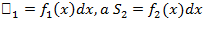. Из этих трех равенств получаем: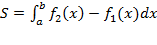 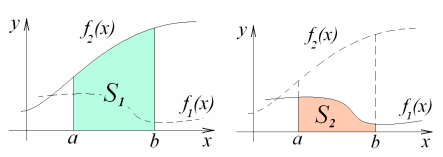. 2. Вычисление длины дуги кривой -Длина дуги: - предел, к к. стрем.длина ломанной линии, вписанной в эту дугу, когда число звеньев ломанной неограниченно возрастает, а длина наиб. звена ее стрем. к 0.Пусть нам требуется вычислить длину дуги кривой между точками A и B, и пусть кривая эта задана одним из 3x способов: • в декартовых координатах: y = f(x), x ∈ [a b]; • в полярных координатах: r = r(ϕ), ϕ ∈ [α, β]; Дифференциалом дуги кривой, заданной в декартовых, полярных координатах, либо параметрическиназ величина dl: • в декартовых координатах: 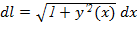; • в полярных координатах: 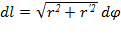; Вычисление площади поверхности вращения Лемма 1.6. Усл. Кривая AB задана равенством y = f(x) 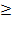0, либо в полярных координатах, либо параметрически. Все функции, входящие в выражение для дифференциала дуги dl непрерывны. Утв. Площадь поверхности, образованной вращением этой кривой вокруг оси Ox, вычисляется по формуле: 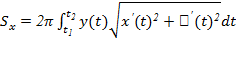. Плоская фигура Q называется квадрируемой, если верхняя площадь 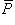этой фигуры совпадает с ее нижней площадью 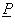. При этом

число 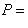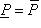называется площадью фигуры Q. Справедлива следующая теорема. Теорема 1. Для того чтобы плоская фигура Q была квадрируемой, необходимо и достаточно, чтобы для любого положительного числа ε можно было указать такой описанный вокруг фигуры Q многоугольник и такой вписанный в фигуру Q многоугольник, разность S_d - S_i площадей которых была бы меньше ε, S_d - S_i < ε. Тело 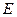называется кубируемым, если верхний объем 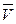этот тела совпадает с нижним объемом 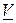. При этом число 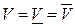называется объемом тела .

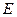Теорема: Для того чтобы тело 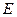было кубируемым, необходимо и достаточно, чтобы для любого положительного числа 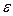можно было указать такой описанный вокруг тела 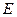многогранник и такой вписанные в тело 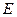многогранник, разность 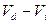объемов которых была бы меньше .

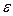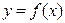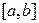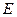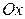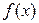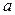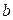Теорема: Пусть функция непрерывна на сегменте . Тогда тело , образованное вращением вокруг оси криволинейной трапеции, ограниченной графиком функции , ординатами в точках и , и отрезком оси 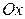между точкам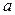и и 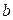, кубируемо и его объем 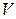может быть найден по формуле

.

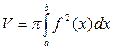Вопрос 9. Числовые ряды.

Числовым рядом (или просто рядом) называется выражение вида 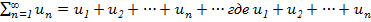– действительные/компленкные числа, наз. Членами рядами, 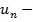общий член ряда. Сумма первых п членов ряда наз n-й частичнойсуммой ряда и обозначается через Sn, т. е. Sn = 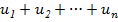Рассмотрим след. частичные суммы: 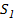= 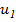. 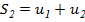, ,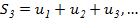,. Если су-ет конечный предел 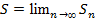последовательности частичных сумм ряда, то этот предел наз суммой ряда и говорят, что ряд сходится. = 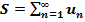. Если 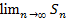не существует или 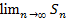= 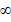) наз расходящимся. Такой ряд суммы не имеет.

Исследуем сходимость ряда а + aq + aq^2 +... + aq^n-1 к. наз рядом геометрической прогрессии. Его частоиспольз.при исследовании рядов на сходимость.

Нахождение п -й частичной суммы Sn и ее предела для произвольного ряда во многих случаях является непростой задачей. Поэтому для выяснения сходимости ряда устанавливают специальные признаки сходимости. Первым из них, как правило, явл необходимый признаксходимости. Т- Если ряд сходится, то его общий член ипстремится к нулю, т е. 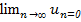След. (достаточное условие расходимости ряда). Еслиlim ип 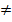0 или этот предел не сущ-ет, то ряд расходится. Необходимый признак сходимости не дает, вообще говоря, возможности

судить о том, сходится ли данный ряд или нет. Сходимость ирасходимость ряда во многих случаях можно установить с помощьютак называемых достаточных признаков. Рассмотрим некоторые из них для знакоположительных рядов,т. е. рядов с неотрицательными членами (знакоотрицательный ряд переходит в знакоположительный путем умножения его на (—1), что, как известно, не влияет на сходимость ряда).1) Признаки сравнения рядов Сходимость или расходимость накоположительного ряда часто устанавливается путем сравнения его с другим (≪эталонным≫) рядом, о которомизвестно, сходитсяонилинет. В основетакогосравнениялежатследующиетеоремы.

Теорема (предельный признак сравнения). Пусть даны два знакоположительных ряда (60 1) и (60 2) Если су-ет конечный, отличный от 0, предел lim 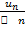= А (0 < А <оо), то ряды (60.1) и (60.2) сходятся или расходятся одновременно. Признак Даламбера В отличие от признаков сравнения, где все зависит от догадки и запаса известных сходящихся и расходящихся рядов, признак Даламбера позволяет часто решить вопрос о сходимости ряда, проделав лишь некоторые операции над самим рядом. Т: Пусть дан ряд (59.1) с положительными членами и существует конечный или бесконечный предел lim 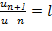Тогда ряд сходится при l < 1 и расходится при l > 1. Радикальный признак Коши Иногда удобно пользоваться радикальным признаком Коши для исследования сходимости знакоположительного ряда. Этот признак во многом схож с признаком Даламбера, о чем говорят его формулировка и доказательство. Т: Пусть дан ряд (59.1) с "+" членами исущ-ет конечный или бесконечный предел 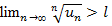Тогда ряд сходится при I < 1 и расходится при I > 1. Интегральный признак Коши.