Несобственные интегралы II рода- Пусть 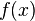 определена на
определена на 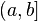 , терпит бесконечный разрыв в точке x=a и
, терпит бесконечный разрыв в точке x=a и 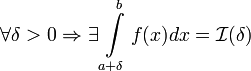
1. Если 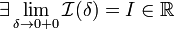 , то используется обозначение
, то используется обозначение 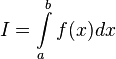 и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
2. Если 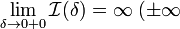 или
или 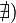 , то обозначение сохраняется, а
, то обозначение сохраняется, а 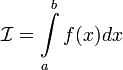 называется расходящимся к
называется расходящимся к 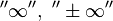 , или просто расходящимся.
, или просто расходящимся.
Пусть 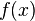 определена на
определена на 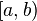 , терпит бесконечный разрыв при x=b и
, терпит бесконечный разрыв при x=b и 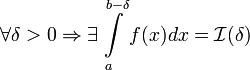 . Тогда:
. Тогда:
1. Если 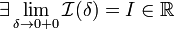 , то используется обозначение
, то используется обозначение 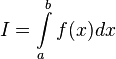 и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
2. Если 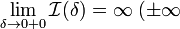 или
или 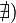 , то обозначение сохраняется, а
, то обозначение сохраняется, а 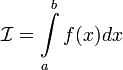 называется расходящимся к
называется расходящимся к 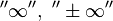 , или просто расходящимся.
, или просто расходящимся.
Если функция 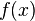 терпит разрыв во внутренней точке
терпит разрыв во внутренней точке  отрезка
отрезка 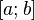 , то несобственный интеграл второго рода определяется формулой:
, то несобственный интеграл второго рода определяется формулой:
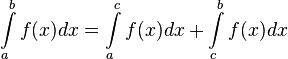
 2015-06-04
2015-06-04 680
680








