Обобщенный гармонический ряд

Рассмотрим з накочередующийся ряд- р яд вида 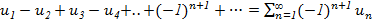Для знакочередующихся рядов имеет место достаточный признак сходимости(лейбница)- знакочередующийся ряд 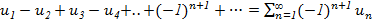сходится, если: 1) последовательность абсолютных величин членов ряда монотонно убывает, т. е. 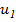> > 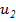> 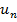ип >...; Общий член ряда стремится к нулю: lim ип = 0При этом сумма S ряда удовлетворяет неравенствам 0<S<u1.

Знакочередующийся ряд явл частным случаем знакопеременного ряда. Числовой ряд ^ ип, содержащий бесконечное множество "+" и бесконечное множество "-" членов, наз знакопеременным.

Д/ знакопеременных рядов имеет место следующий общий достаточный признак сходимости. Т: Пусть дан знакопеременный ряд 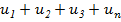. Если сходится ряд | 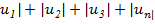составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд. Знакопеременный ряд называется абсолютно сходящимся, если ряд, составленный из модулей его членов, сходится. Знакопеременный ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.