Сравнение средних значений не всегда позволяет составить полную картину изучаемого явления, поскольку может быть так, что средние значения приблизительно равны, а дисперсии отличаются значительно. Поэтому в некоторых случаях кроме критерия Стьюдента целесообразно использовать критерий Фишера. Если оба критерия дают одинаковый статистический вывод, то это позволяет с большей уверенностью сделать окончательный вывод для исследования.
Гипотезы:
Н0: дисперсии исследуемых выборок статистически одинаковы.
Н1: дисперсии статистических выборок статистически различны (не одинаковы).
Н0: "D1 = D2"
H1: "D1 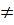 D2"
D2"
Находим значение F критерия Фишера по формуле:
Fэ = 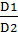 , где D1 – большая, а D2 – меньшая.
, где D1 – большая, а D2 – меньшая.
По таблице критических значений для числа d 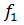 =
= 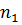 -1 степеней свободы в числителе и числа d
-1 степеней свободы в числителе и числа d 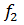 =
= 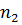 -1 степеней свободы в знаменателе находим:
-1 степеней свободы в знаменателе находим:
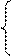 F, р = 0,05
F, р = 0,05
Fкр. =
F, р = 0,01
Fэ 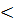 Fкр. =
Fкр. = 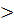 Н0
Н0
Fэ 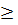 Fкр. =
Fкр. = 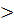 Н1
Н1
Замечание:
Критерий Стьюдента и критерий Фишера можно применять только в том случае, если сравниваемые выборки имеют нормальное распределение, поэтому, прежде, чем их применять, необходимо убедиться в нормальности распределения с помощью метода Плохинского или метода Пустыльника.
 2015-06-04
2015-06-04 2980
2980
