2015-06-04
13864
Интуитивное представление о непрерывной функции обычно связывают с такой функцией, график которой — непрерывная линия.
Определение 1. Функция 
называется непрерывной в точке 
, если выполняются следующие три условия:
1) функция определена в точке , т. е. 
;
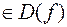2) существует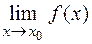 
;
3) 
.
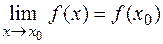Если в точке нарушено хотя бы одно из условий 1—3, то функция называется разрывной в точке , а точка — точкой разрыва.
Если воспользоваться определением предела функции в точке по Коши, то можно дать эквивалентное определение непрерывной функции в точке на языке «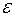
— 
».
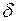Определение 2. Функция 
называется непрерывной в точке , если для любого заданного числа 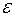> 0 можно найти такое число 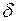> О (зависящее от 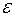и ), что для всех 
, для которых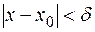 
, будет выполняться неравенство 
.
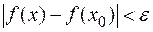В более краткой записи определение можно записать так:
непрерывна в точке 
.
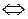
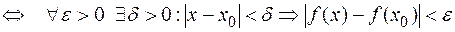Так как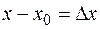 
— приращение аргумента, a 
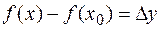— приращение функции в точке , то определение 2 можно сформулировать следующим образом: функция непрерывна в точке , если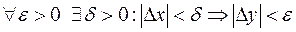 
, т.е. 
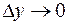при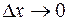 
. Таким образом, получаем еще одно определение непрерывности.
Определение 3. Функция называется непрерывной в точке , если бесконечно малому приращению аргумента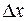 
соответствует бесконечно малое приращение функции 
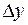, т. е. 
.
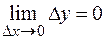В некоторых случаях приходится пользоваться понятием односторонней непрерывности.
Определение. Функция , определенная в некоторой левой (правой) окрестности точки , называется непрерывной слева (справа) в точке , если существует предел слева (справа) функции и он равен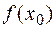 
.
Другими словами,
непрерывна справа в точке 
,
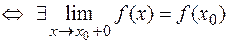непрерывна слева в точке 
.
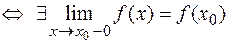Из определения односторонней непрерывности в точке следует, что функция , определенная в некоторой 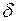-окрестности точки , непрерывна в точке тогда и только тогда, когда она непрерывна в этой точке слева и справа.
Определение. Функция , непрерывная во всех точках некоторого множества X, называется непрерывной на этом множестве.
Если X =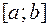 
, то для непрерывности функции на 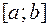требуется, чтобы была непрерывна во всех внутренних точках отрезка, непрерывна справа на левом его конце, т. е. в точке а, и непрерывна слева на правом его конце, т. е. в точке b.
