Непрерывность основных элементарных функций

Сформулируем теоремы о непрерывности функций, полученных в результате арифметических действий над непрерывными функциями, а также их композиции.

Доказательства этих теорем однотипны и основываются на опре­делении непрерывности функции в точке.

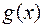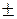
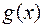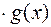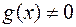Теорема. Если функции и непрерывны в точке , то и функции , непрерывны в точке . Если, кроме того, , то функция / 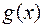является также непрерывной в точке .

Доказательство. Докажем, например, непрерывность функции 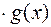в точке . Из непрерывности функций и 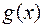в точке следует, что 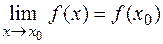, 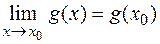. Тогда

.

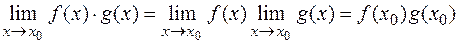т. е. функция 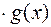непрерывна в точке . Аналогично доказы­ваются другие утверждения теоремы.

⊠

Эту теорему можно обобщить на случай конечного числа функ­ций: алгебраическая сумма и произведение конечного числа функций, непрерывных в точке х₀, непрерывны в точке .

Сформулируем теорему о непрерывности сложной функции.

Теорема. Сложная функция, являющаяся композицией ко­нечного числа непрерывных в точке функций, непрерывна в точке .

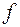Доказательство. Докажем эту теорему для случая, когда сложная функция является композицией двух непрерывных в точке функций и .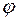

Пусть 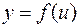, , 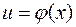тогда по определению сложной функции

.

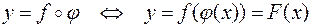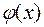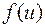Теорема утверждает, что если функция непрерывна в точке , а функция непрерывна в точке 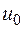, то сложная функция 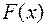непрерывна в точке .

Действительно, пусть 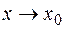. Тогда из непрерывности функции 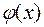следует, что 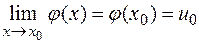, т. е. что 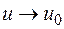. Поскольку

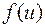непрерывна в точке 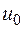, то 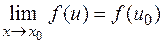Но так как 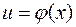, то последнее равенство можно записать в виде

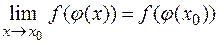
или

.

⊠

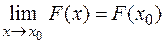Из определения 1 непрерывной функции в точке и последней теоремы следует, что

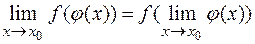
или в частном случае

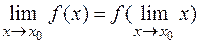
т. е. символы предела и непрерывной функции перестановочны.

Приведем без доказательства следующие две теоремы.

Теорема. Пусть функция определена, непрерывна и монотонна на некотором множестве X и пусть Y — множество ее значений. Тогда на множестве Y обратная функция 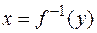моно­тонна и непрерывна.

Теорема. Основные элементарные функции непрерывны во всех точках, принадлежащих их области определения.