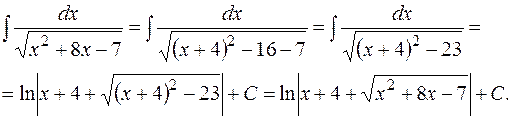
Интегралы вида 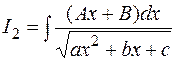 . В числителе интеграла
. В числителе интеграла 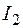 выделяется дифференциал выражения, стоящего под знаком радикала, и этот интеграл представляется в виде суммы двух интегралов:
выделяется дифференциал выражения, стоящего под знаком радикала, и этот интеграл представляется в виде суммы двух интегралов:
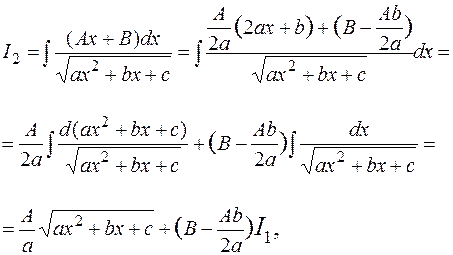
где 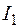 — вычисленный выше интеграл.
— вычисленный выше интеграл.
Пример. Найти 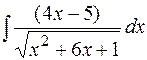 .
.
Решение. Имеем интеграл вида 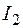 :
:
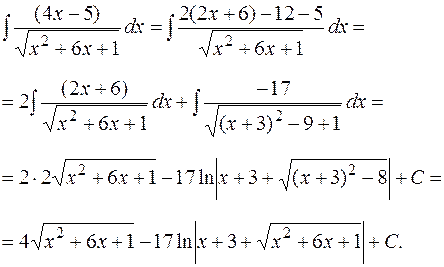
Интегралы вида 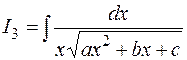 . Вычисление интеграла
. Вычисление интеграла 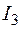 сводится к вычислению
сводится к вычислению 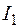 , подстановкой:
, подстановкой: 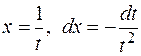 .
.
Пример. Найти 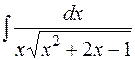 .
.
Решение. Имеем интеграл вида 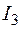 :
:
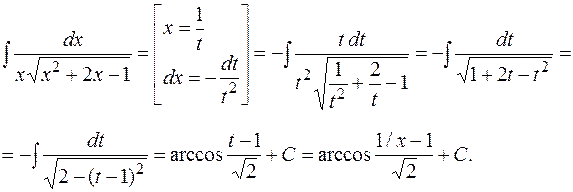
Интегралы вида 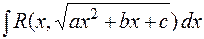 . Существует несколько различных приемов их вычисления, рассмотрим один из таких приемов, основанный на применении тригонометрических подстановок.
. Существует несколько различных приемов их вычисления, рассмотрим один из таких приемов, основанный на применении тригонометрических подстановок.
Квадратный трехчлен 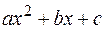 путем выделения полного квадрата и замены переменной может быть представлен в виде
путем выделения полного квадрата и замены переменной может быть представлен в виде 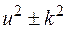 . Таким образом, достаточно ограничиться рассмотрением трех видов интегралов:
. Таким образом, достаточно ограничиться рассмотрением трех видов интегралов:
1) Интеграл 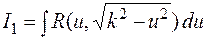 подстановкой
подстановкой 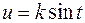 (или
(или 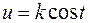 ) сводится к интегралу от рациональной функции относительно
) сводится к интегралу от рациональной функции относительно 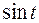 и
и 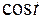 .
.
Действительно, применим, например, подстановку 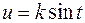 (
(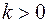 ), тогда
), тогда 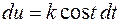 ,
, 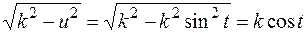 ,
,
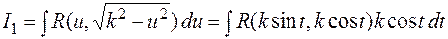 .
.
2) Интеграл 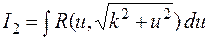 подстановкой
подстановкой 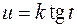 (или
(или 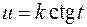 ) сводится к интегралу от рациональной функции относительно
) сводится к интегралу от рациональной функции относительно 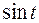 и
и 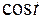 .
.
3) Интеграл 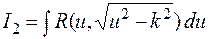 подстановкой
подстановкой 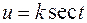 (или
(или 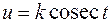 ) также сводится к интегралу от рациональной функции относительно
) также сводится к интегралу от рациональной функции относительно 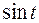 и
и 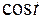 .
.
Пример. Найти 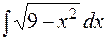 .
.
 2015-06-04
2015-06-04 1892
1892
