Геометрический смысл определенного интеграла

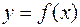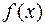Пусть функция непрерывна на отрезке и r0.

Определение. Фигура, ограни­ченная графиком АВ функции 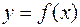, прямыми 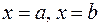и осью 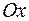, называется криволинейной трапецией.

Интегральная сумма и ее слагаемые имеют простой геометри­ческий смысл: произведение 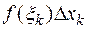равно площади прямоуголь­ника с основанием 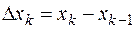и высотой 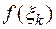, а сумма 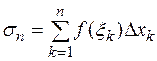представляет собой площадь заштрихованной ступенчатой фигуры, изображенной на рисунке.

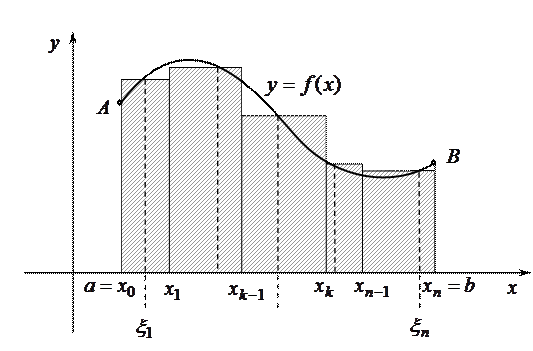
Очевидно, что эта площадь зависит от разбиения 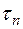отрезка на частичные отрезки и вы­бора точек .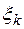

Чем меньше 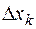, 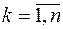тем площадь ступенчатой фигуры ближе к площади криволинейной трапеции. Следовательно, за точ­ную площадь 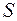криволинейной трапеции принимается предел инте­гральной суммы при :

.

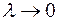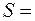
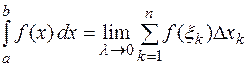Таким образом, с геометрической точки зрения определенный интеграл от неотрицательной функции численно равен площади соответствующей криволинейной трапеции.