Рассмотрим свойства определенного интеграла, доказательство которых основывается на определении определенного интеграла.
1. Если нижний и верхний пределы интегрирования равны (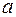 =
= 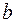 ), то интеграл равен нулю:
), то интеграл равен нулю:
2. Если  = 1, то
= 1, то
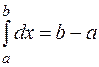
3. При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:
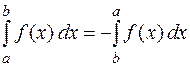
4. Постоянный множитель можно выносить за знак определенного интеграла:
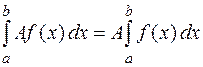 .
.
5. Определенный интеграл от алгебраической суммы конечного числа интегрируемых на  функций
функций 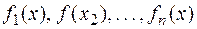 равен алгебраической сумме определенных интегралов от слагаемых:
равен алгебраической сумме определенных интегралов от слагаемых: 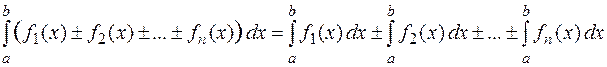 .
.
6( Аддитивность определенного интеграла). Если существуют интегралы 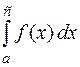 и
и 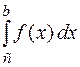 , то существует также интеграл
, то существует также интеграл 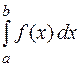 и для любых чисел
и для любых чисел 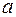 ,
, 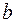 ,
, 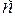
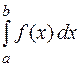
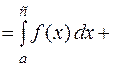
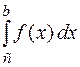 .
.
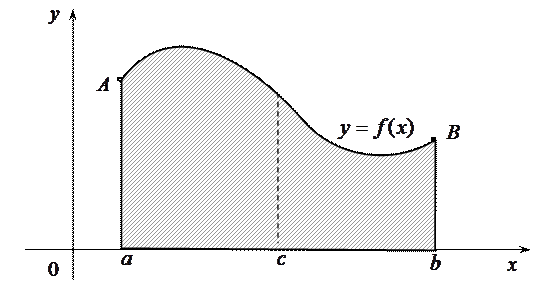
Геометрический смысл свойства 6 состоит в том, что площадь криволинейной трапеции с основанием  равна сумме площадей криволинейных трапеций с основаниями
равна сумме площадей криволинейных трапеций с основаниями 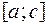 и
и 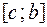 .
.
7. Если  r0 для
r0 для 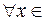
 , то
, то
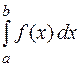 r0, (
r0, (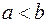 )
)
8 (Монотонность определенного интеграла). Если интегрируемые функции  и
и 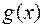 удовлетворяют неравенству
удовлетворяют неравенству  r
r 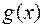 для
для 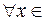
 , то
, то
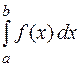 r
r 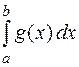 , (
, (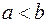 )
)
9 (Об оценке определенного интеграла). Если 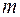 и
и 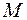 — соответственно наименьшее и наибольшее значения функции
— соответственно наименьшее и наибольшее значения функции  , непрерывной на отрезке
, непрерывной на отрезке  , то
, то
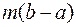 b
b 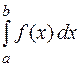 b
b 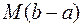 . (1)
. (1)
Доказательство. По условию 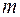 b
b  b
b 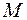 для
для 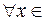
 , следовательно, по свойству 8
, следовательно, по свойству 8
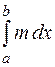 b
b 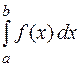 b
b 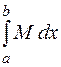
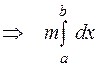 b
b 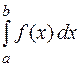 b
b 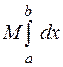 ,
,
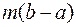 b
b 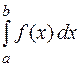 b
b 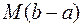 .
.
⊠
На рисунке дана геометрическая интерпретация свойства 9 в случае, когда  r0
r0 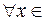
 . Площадь прямоугольника
. Площадь прямоугольника 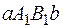 равна
равна 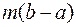 , площадь прямоугольника
, площадь прямоугольника 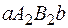 равна
равна 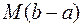 . Из неравенства (1) следует, что площадь криволинейной трапеции
. Из неравенства (1) следует, что площадь криволинейной трапеции 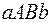 не меньше площади первого прямоугольника и не больше площади второго.
не меньше площади первого прямоугольника и не больше площади второго.
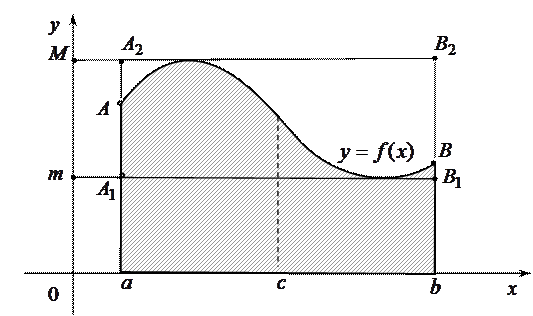
10 (Теорема о среднем). Если функция  непрерывна на отрезке
непрерывна на отрезке  , то существует такая точка
, то существует такая точка 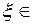
 , что
, что
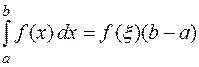 . (2)
. (2)
т. е. определенный интеграл от непрерывной функции равен произведению значения подынтегральной функции в некоторой промежуточной точке отрезка интегрирования  и длины
и длины 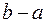 этого отрезка.
этого отрезка.
Доказательство. Так как  непрерывна на отрезке
непрерывна на отрезке  , то она по теореме Вейерштрасса достигает на
, то она по теореме Вейерштрасса достигает на  своего наименьшего
своего наименьшего 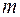 и наибольшего
и наибольшего 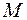 значений, т. е.
значений, т. е.
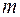 b
b  b
b 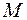 для
для 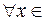
 .
.
Из данного неравенства на основании свойства 9 имеем
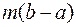 b
b 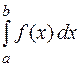 b
b 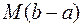 .
.
Разделив все члены двойного неравенства на 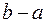 > 0, получим
> 0, получим
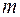 b
b 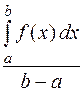 b
b 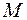
Обозначим 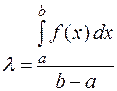 , тогда
, тогда 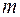 b
b 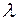 b
b 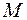 .
.
Другими словами, число 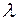 находится между наименьшим и наибольшим значениями функции
находится между наименьшим и наибольшим значениями функции  . Поскольку непрерывная на отрезке
. Поскольку непрерывная на отрезке  функция
функция  по теореме Больцано-Коши принимает все промежуточные значения, лежащие между
по теореме Больцано-Коши принимает все промежуточные значения, лежащие между 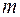 и
и 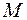 , в том числе и значение
, в том числе и значение 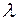 , то существует
, то существует 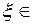
 , такое, что
, такое, что 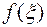 =
= 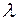 , то есть
, то есть
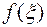
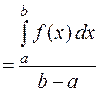 ,
, 
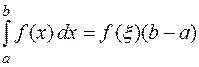 .
.
⊠
Число 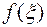 при этом называется интегральным средним значением функции
при этом называется интегральным средним значением функции  на отрезке
на отрезке  .
.
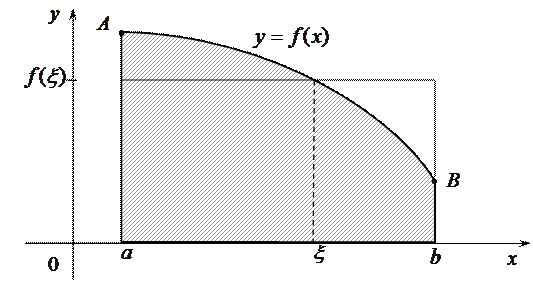
На рисунке дана геометрическая интерпретация свойства 10 в случае, когда  > 0
> 0 
 . Так как значение
. Так как значение 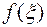 (
(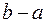 ) численно равно площади прямоугольника с основанием
) численно равно площади прямоугольника с основанием 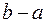 и высотой
и высотой 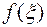 , то теорема о среднем утверждает, что существует прямоугольник, равновеликий криволинейной трапеции
, то теорема о среднем утверждает, что существует прямоугольник, равновеликий криволинейной трапеции 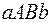 .
.
 2015-06-04
2015-06-04 1657
1657
